二类相变和Ising模型中的相变有什么关系,如何判断临界温度?
参考资料
参考资料



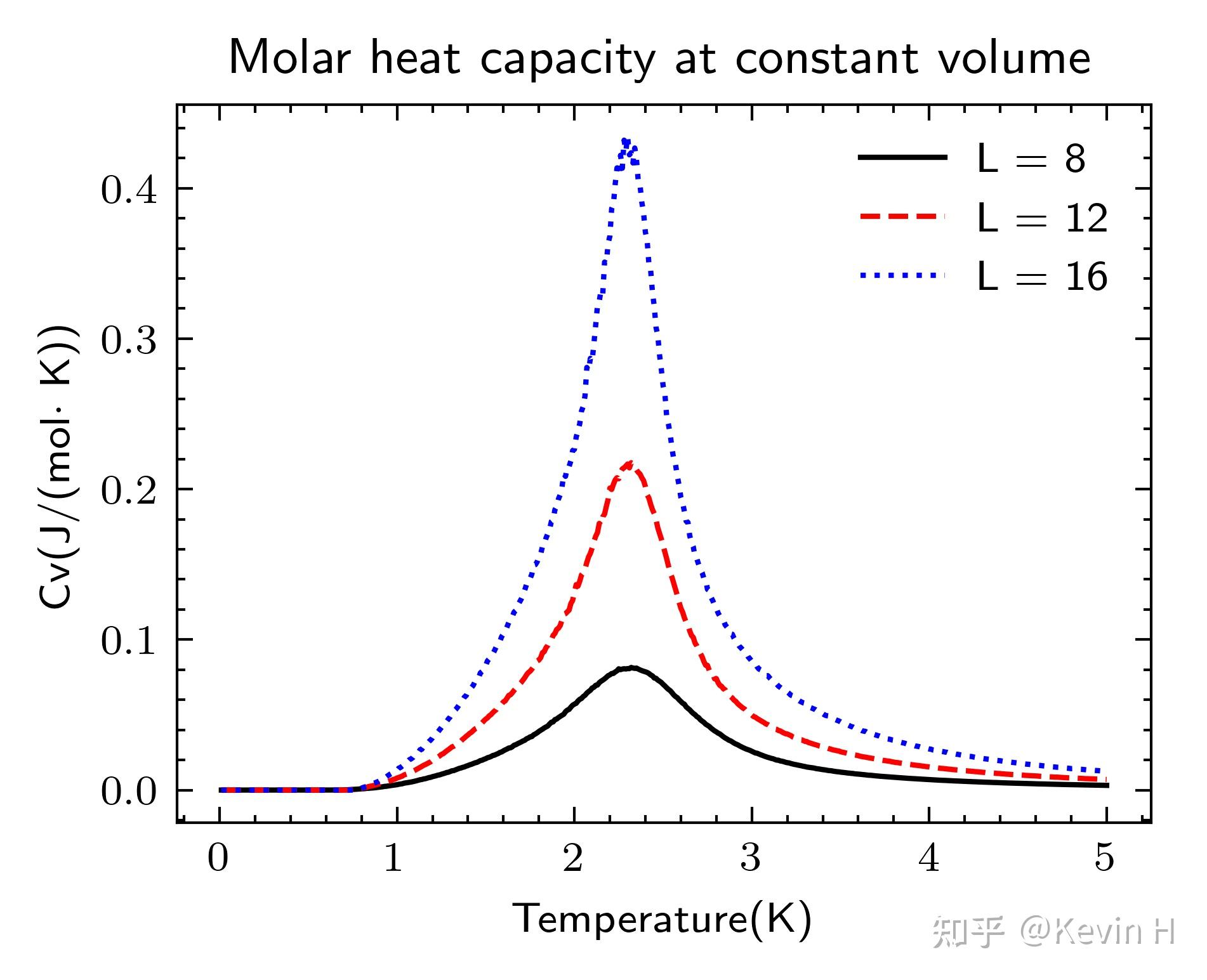
Moonshot回答
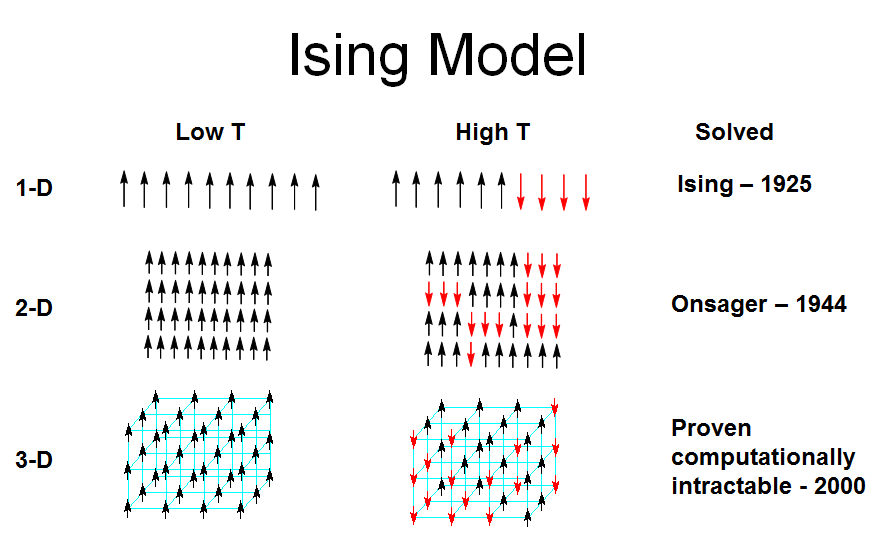
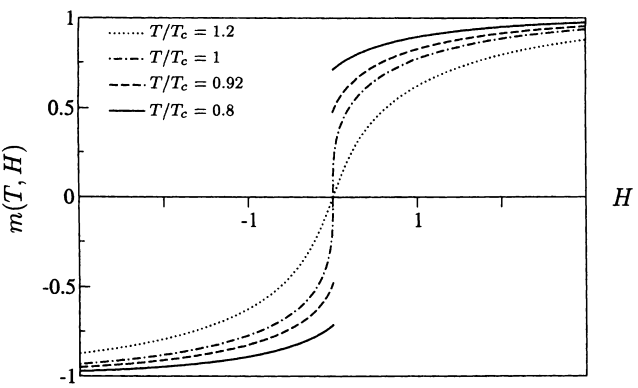
二类相变和Ising模型中的相变有密切的关系。二类相变指的是相变过程中序参量连续变化,而物理量的变化率(如热容、比热容等)发散的相变。Ising模型是一个描述物质相变的数学模型,它通过自旋变量来模拟物质内部原子的磁性状态,从而研究铁磁质的相变现象。Ising模型中的相变是一种典型的二类相变,因为在这个模型中,系统的磁化率在临界温度附近会出现发散行为。
判断Ising模型的临界温度通常有以下几种方法:
-
解析方法:对于某些特殊情况,如一维和二维的Ising模型,可以通过解析方法得到临界温度的精确值。例如,二维正方形晶格Ising模型的临界温度是$T_c = 2J/\ln(\sqrt{2}+1)$,其中$J$是最近邻自旋之间的交换作用能量。
-
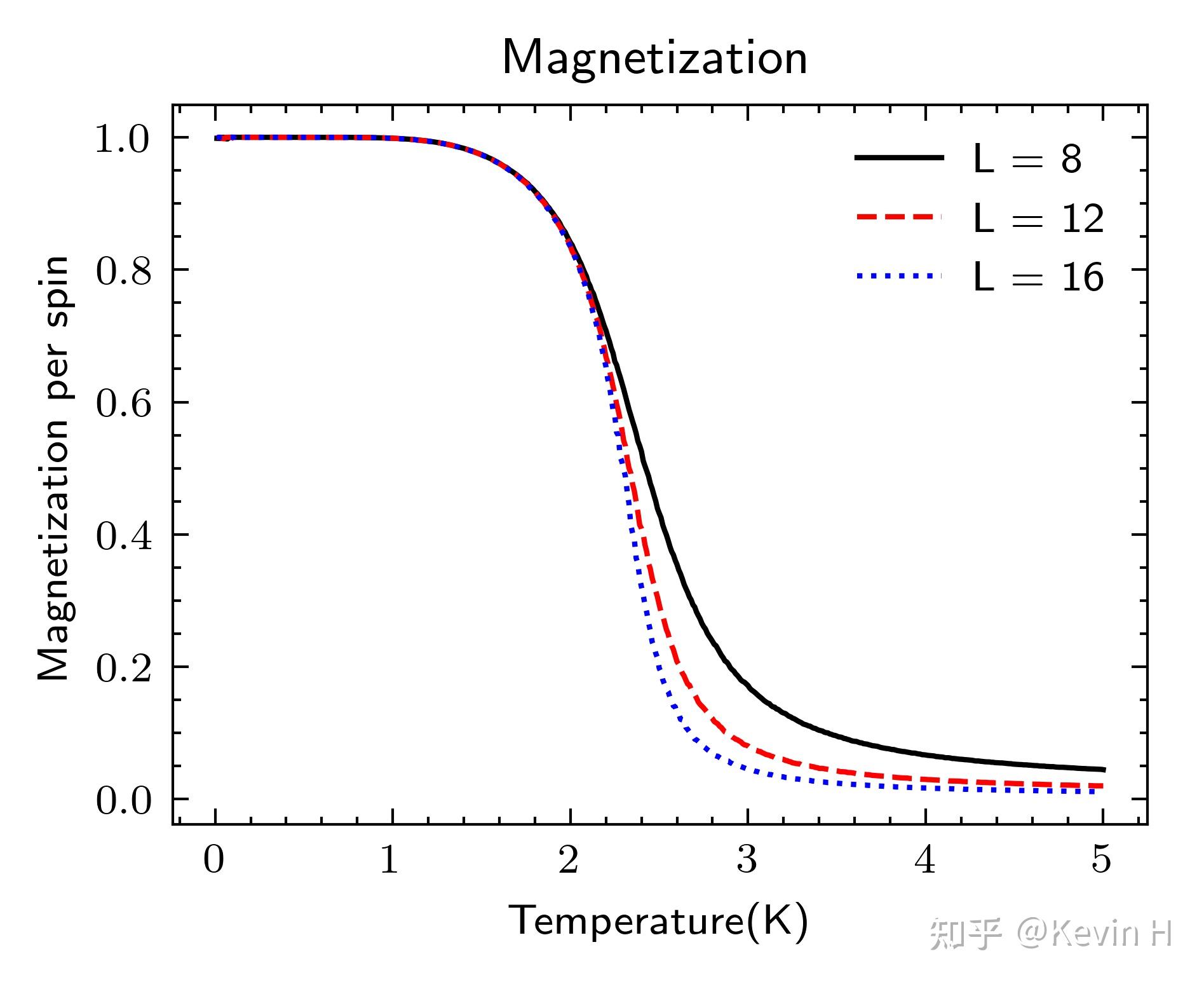
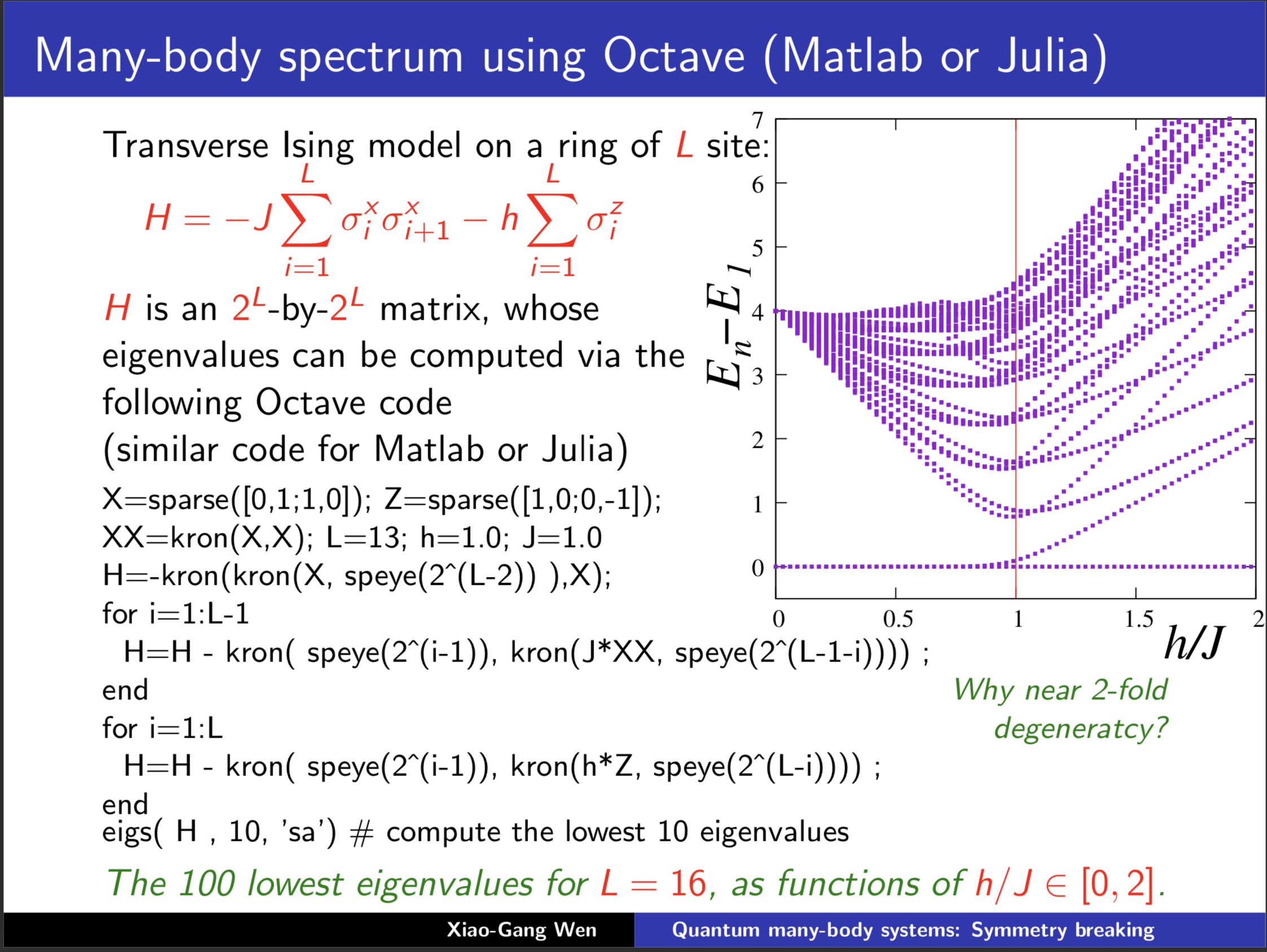
数值模拟:对于更高维度的模型,解析方法往往难以应用,这时可以采用蒙特卡洛模拟等数值方法来估算临界温度。通过模拟系统在不同温度下的自旋排列,可以观察到系统行为的变化,从而确定临界点。
-
实验测量:在实际的物理系统中,通过实验测量物质的磁性随温度的变化,可以确定系统的临界温度。
-
理论估算:根据统计物理中的理论,可以对临界温度进行估算。例如,通过耦合技巧将Ising模型与接触过程联系起来,可以得到临界温度的上界。
在实际应用中,临界温度的确定往往需要结合理论分析和实验数据。通过这些方法,我们可以更准确地理解和预测物质的相变行为。