转动惯量和旋转动力学有什么关系,它们在物理学中的意义是什么?
参考资料


Moonshot回答
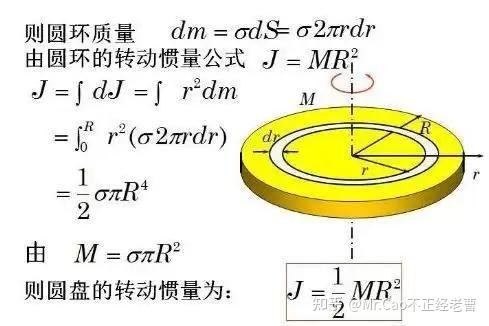
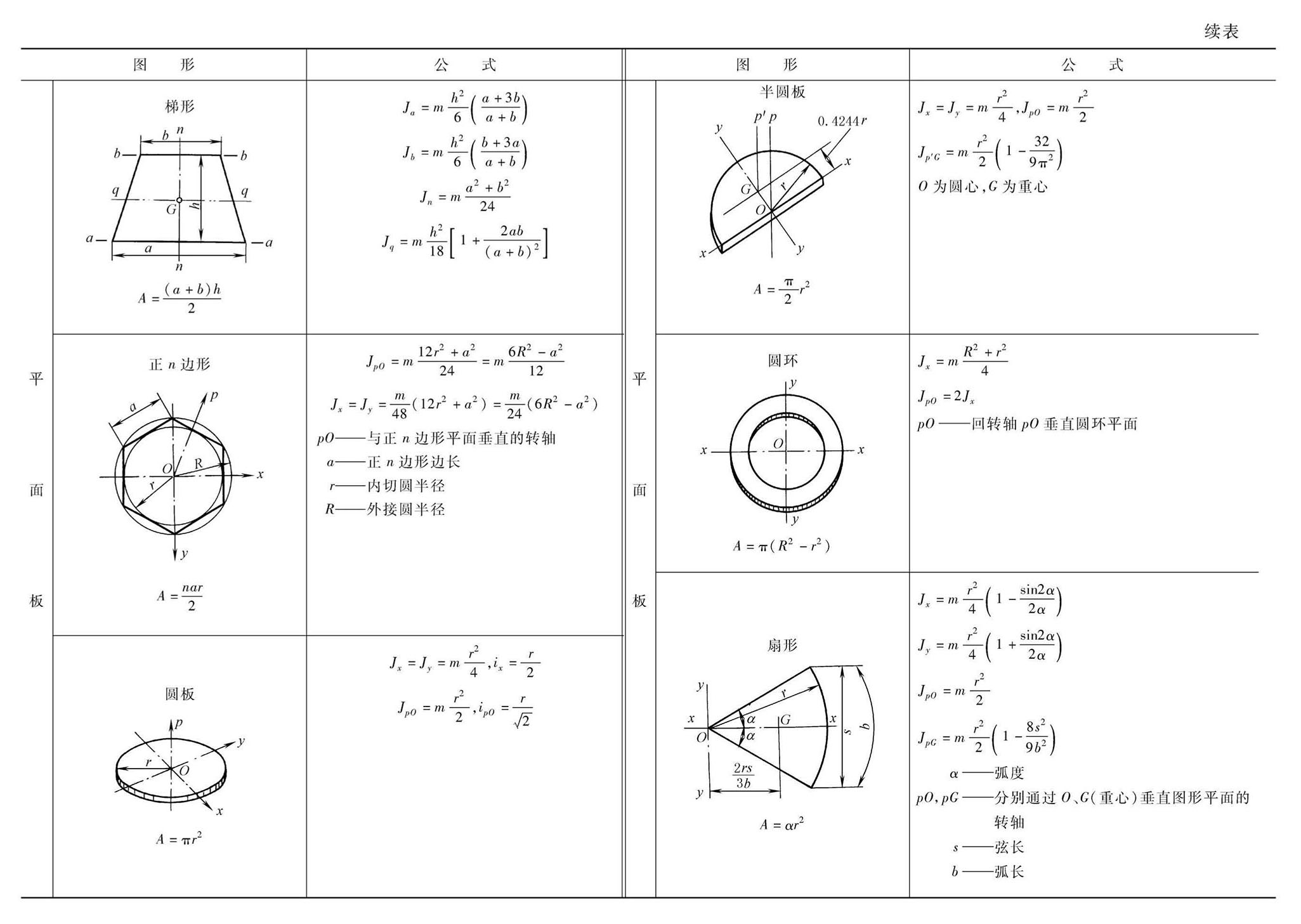
转动惯量和旋转动力学在物理学中有着密切的关系。转动惯量是衡量物体对旋转运动的惯性大小的量度,它在旋转动力学中的角色相当于线性动力学中的质量。转动惯量用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
转动惯量在物理学中的意义非常重要,它在科学实验、工程技术、航天、电力、机械、仪表等领域都有广泛的应用。例如,在航天领域,转动惯量对于卫星和航天器的稳定性和控制至关重要。在机械工程中,转动惯量对于设计旋转机械如发动机、涡轮机等非常关键,因为它们影响机械的动态性能和效率。
此外,转动惯量也与角动量守恒定律相关,即如果没有外力矩作用,一个物体的角动量保持不变。这在分析旋转系统的动力学行为时非常重要。
以下是一些与转动惯量和旋转动力学相关的图片,可以帮助直观理解这些概念:
这些图片展示了转动惯量在不同情况下的计算和应用,以及它如何影响物体的旋转运动。
