参考资料

菲涅尔衍射和夫琅禾费衍射是光学中描述光波遇到障碍物时发生弯曲和扩散的两种不同情况。它们的主要区别在于光波与障碍物之间的距离以及衍射图样的观测条件。

1. 衍射距离：

   • 菲涅尔衍射：发生在光源、障碍物和观察点之间的距离都是有限的，即近场衍射。菲涅尔衍射考虑了波前的曲率，适用于光波在有限距离内的衍射现象。
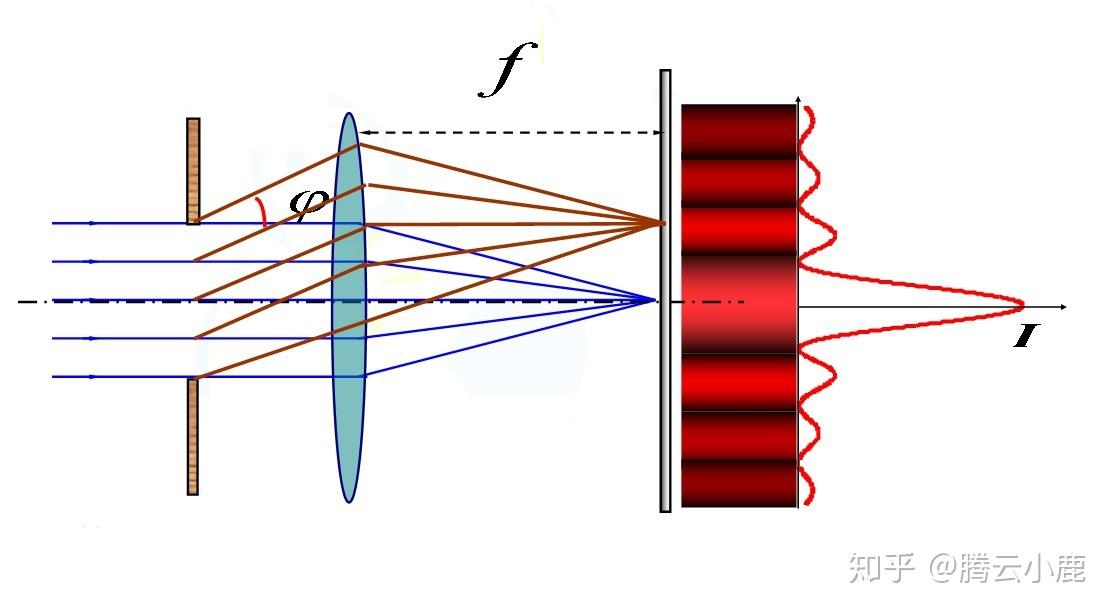
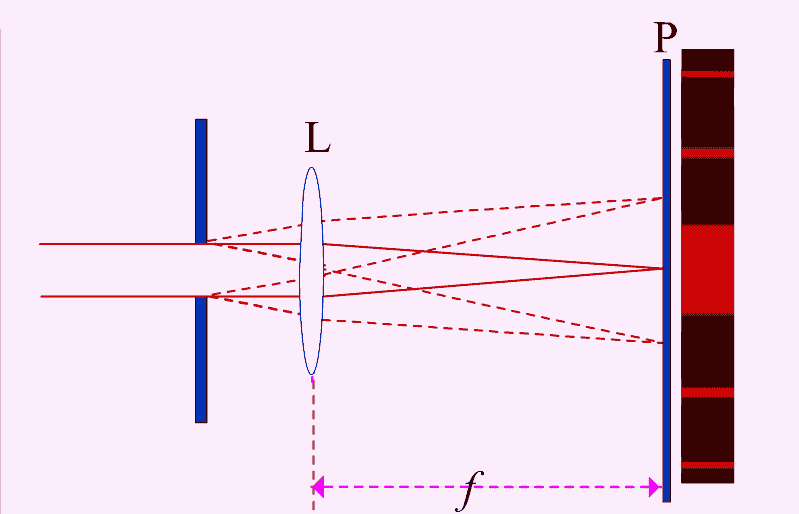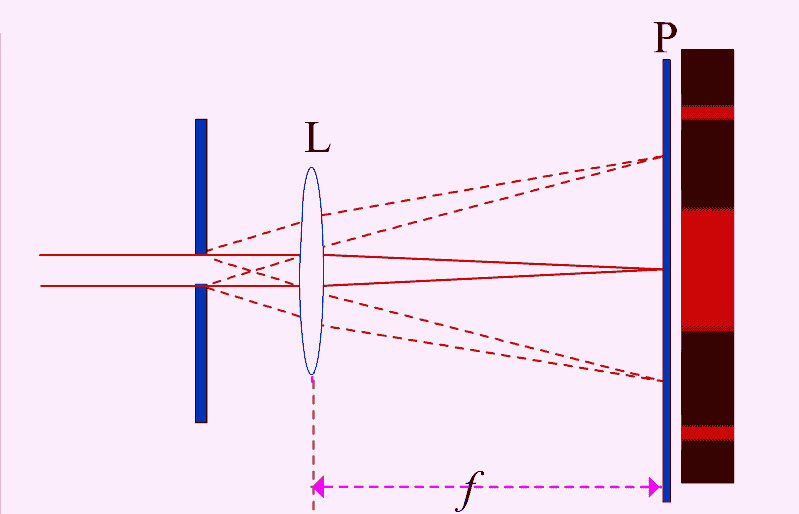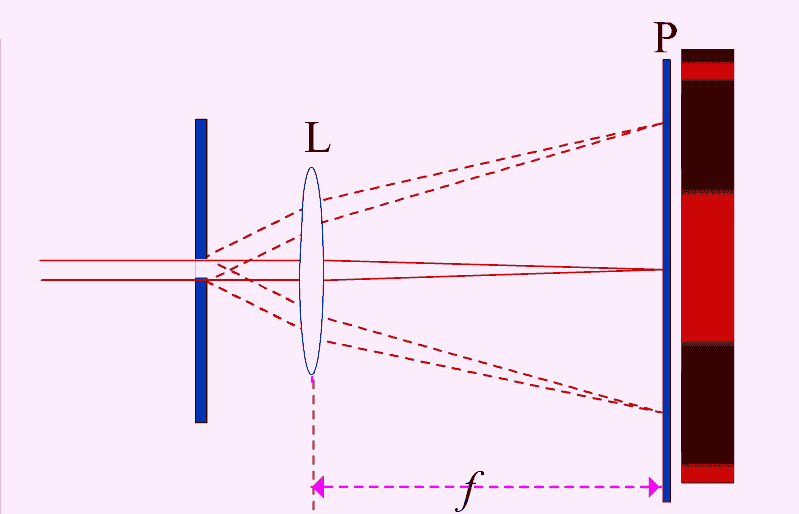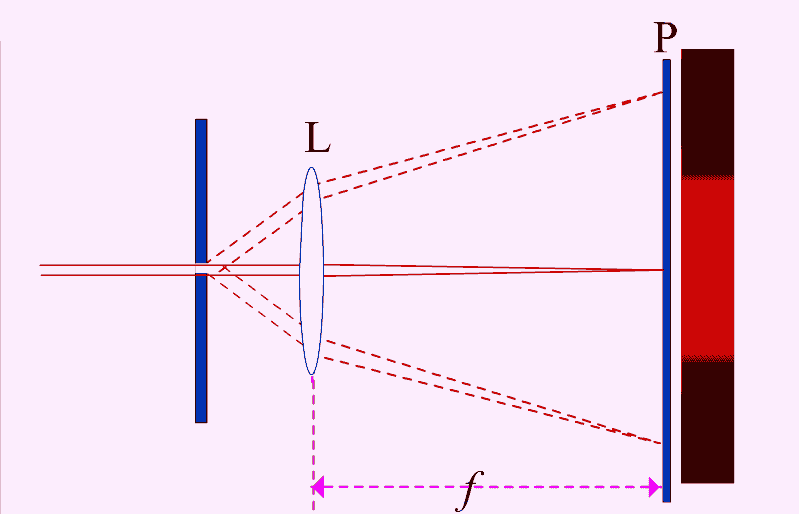
   • 夫琅禾费衍射：发生在光源或障碍物到观察点的距离至少有一个是无限远的情况，即远场衍射。夫琅禾费衍射假设入射光和衍射光都是平行光束，适用于描述通过圆孔或狭缝的光波。

2. 实验现象：

   • 菲涅尔衍射：成像的大小和形状会受到影响，并且只有在特定条件下（菲涅尔数远小于1）才会发生。
   • 夫琅禾费衍射：通常通过将观察屏放到透镜的焦平面上来简单获得远场条件，适用于成像光学中的聚焦位置。

3. 数学处理：

   • 菲涅尔衍射：需要使用菲涅尔积分来计算光波的衍射图样，这涉及到对波前曲率的考虑。
   • 夫琅禾费衍射：可以使用惠更斯-菲涅尔原理，通过衍射图样的傅里叶变换来计算，这通常简化了数学处理。

4. 实际举例：

   • 菲涅尔衍射：例如，激光束经过一个狭缝后形成的衍射图样。
   • 夫琅禾费衍射：例如，通过望远镜观察遥远星系时，星系发出的光可以被视为平行光束，产生的衍射现象。

总的来说，菲涅尔衍射和夫琅禾费衍射的主要区别在于它们适用的物理条件和数学处理方式。菲涅尔衍射适用于近场条件，而夫琅禾费衍射适用于远场条件。两者都是描述光波衍射现象的重要概念。