参考资料

连续性方程在大气科学中体现质量守恒原理的方式是将质量守恒定律应用于流体力学。它表明，在没有质量源或汇的情况下，流体的密度与其速度的乘积（即质量通量）在空间中任意闭合表面上的净流出量必须为零。这意味着流体在某一区域的增加量必须由另一区域的减少量来平衡，从而确保总质量守恒。

连续性方程的一般形式是： [ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0 ] 其中，(\rho) 是流体的密度，(\mathbf{u}) 是流体的速度向量，(\nabla \cdot) 是散度算子。

在大气科学中，连续性方程通常用于研究大气运动，如风、气压系统和天气模式。它帮助科学家和气象学家理解大气中质量的传输和分布，以及如何影响天气和气候现象。

此外，连续性方程在大气模式中也非常重要。通过将研究区域划分成网格，连续性方程帮助模拟大气中的质量守恒。例如，有研究提出使用比容代替温度变量，并以地面气压本身作为展谱变量，以保持大气总质量守恒。

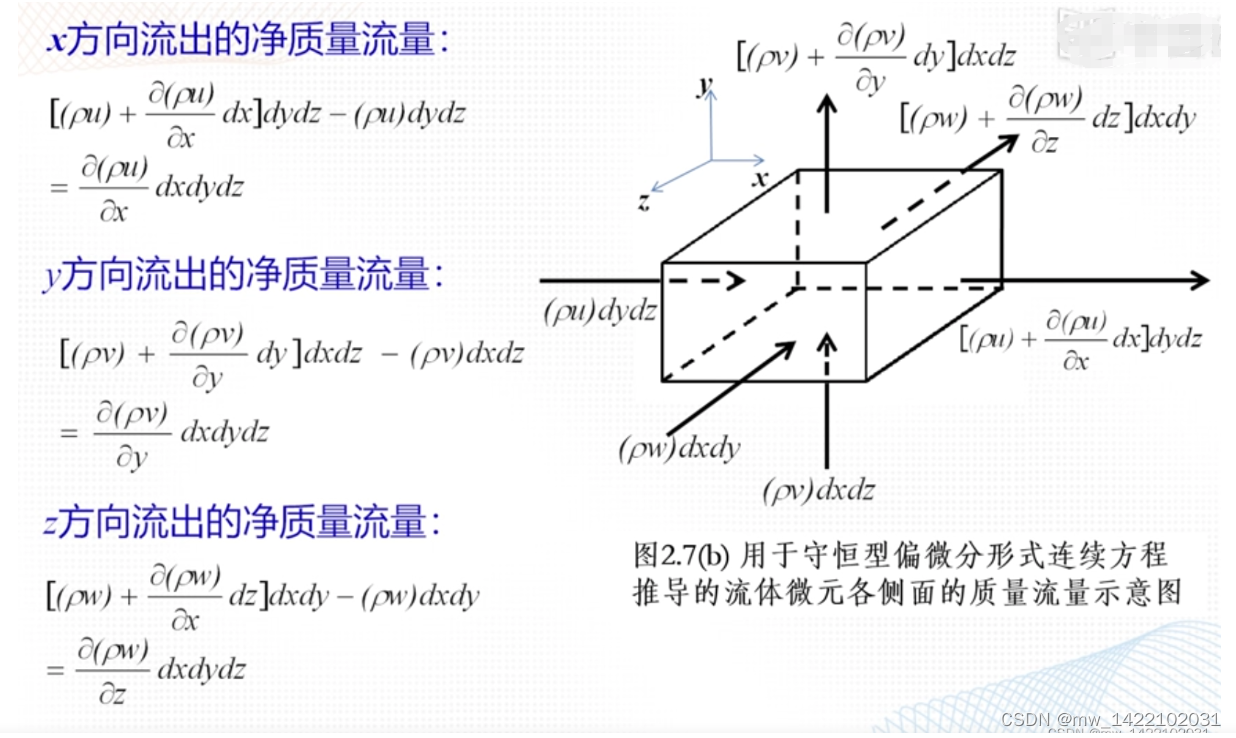
这张图展示了连续性方程在描述流体运动中质量守恒的基本原理。通过这种方式，连续性方程在大气科学中体现了质量守恒的原理。