λ为本征值时,为什么有|λ|^2=1的约束条件?
参考资料
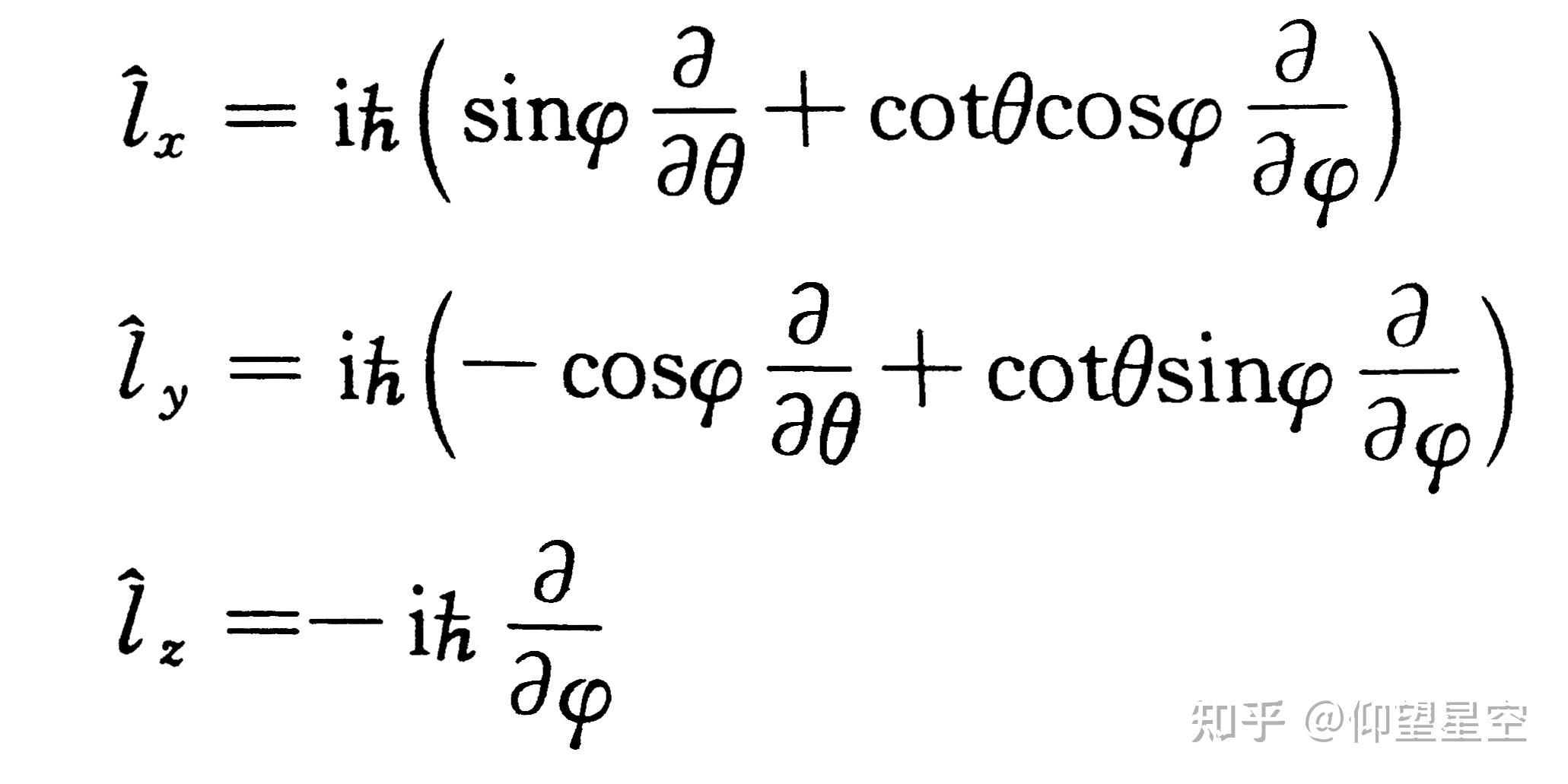

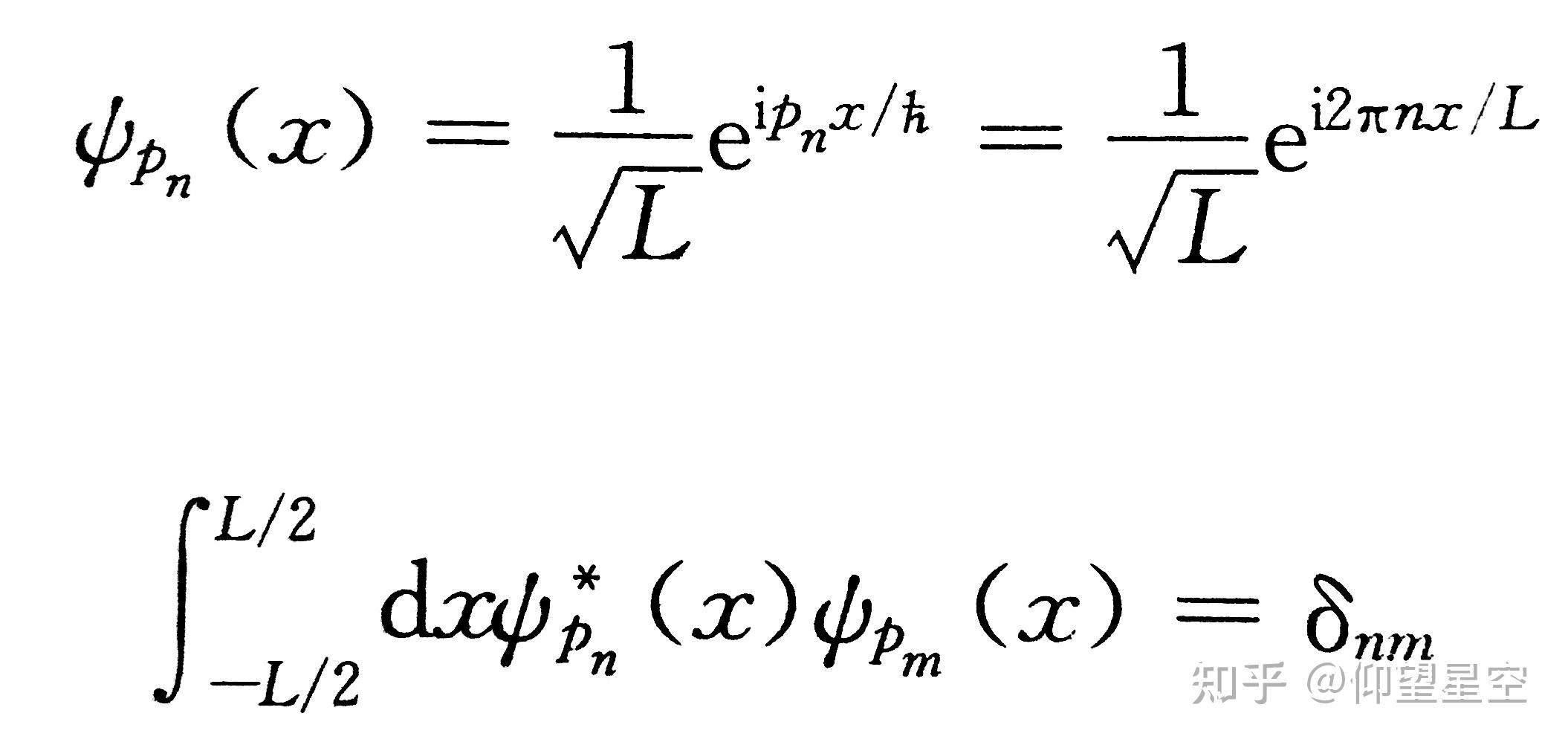
Moonshot回答
在数学和物理学中,本征值(特征值)是一个标量,它描述了线性算子或矩阵对某个向量(本征向量)的作用效果。当一个本征值的模的平方(|λ|^2)等于1时,这通常意味着该线性算子代表的变换是酉变换(在量子力学中,这对应于一个物理可观测量的演化)。
酉变换具有保持向量内积不变的性质,即变换前后向量的模长不变。在量子力学中,这对应于物理可观测量的概率解释,即测量结果的概率幅在变换前后保持不变。因此,|λ|^2=1的约束条件确保了量子态在时间演化过程中保持归一化,这是量子力学的一个基本要求。
此外,本征值问题在物理中非常有用且普遍,因为一个矩阵(算符)的本征值谱是存储全部矩阵信息的最紧凑表示。在某些应用中,选择特定表示是很重要的,因此我们还需要记录本征矢量来联系其它表示和本征值表示(对角矩阵)。但因为对角形式下矩阵元素最少,所以本征值问题在物理中非常重要。
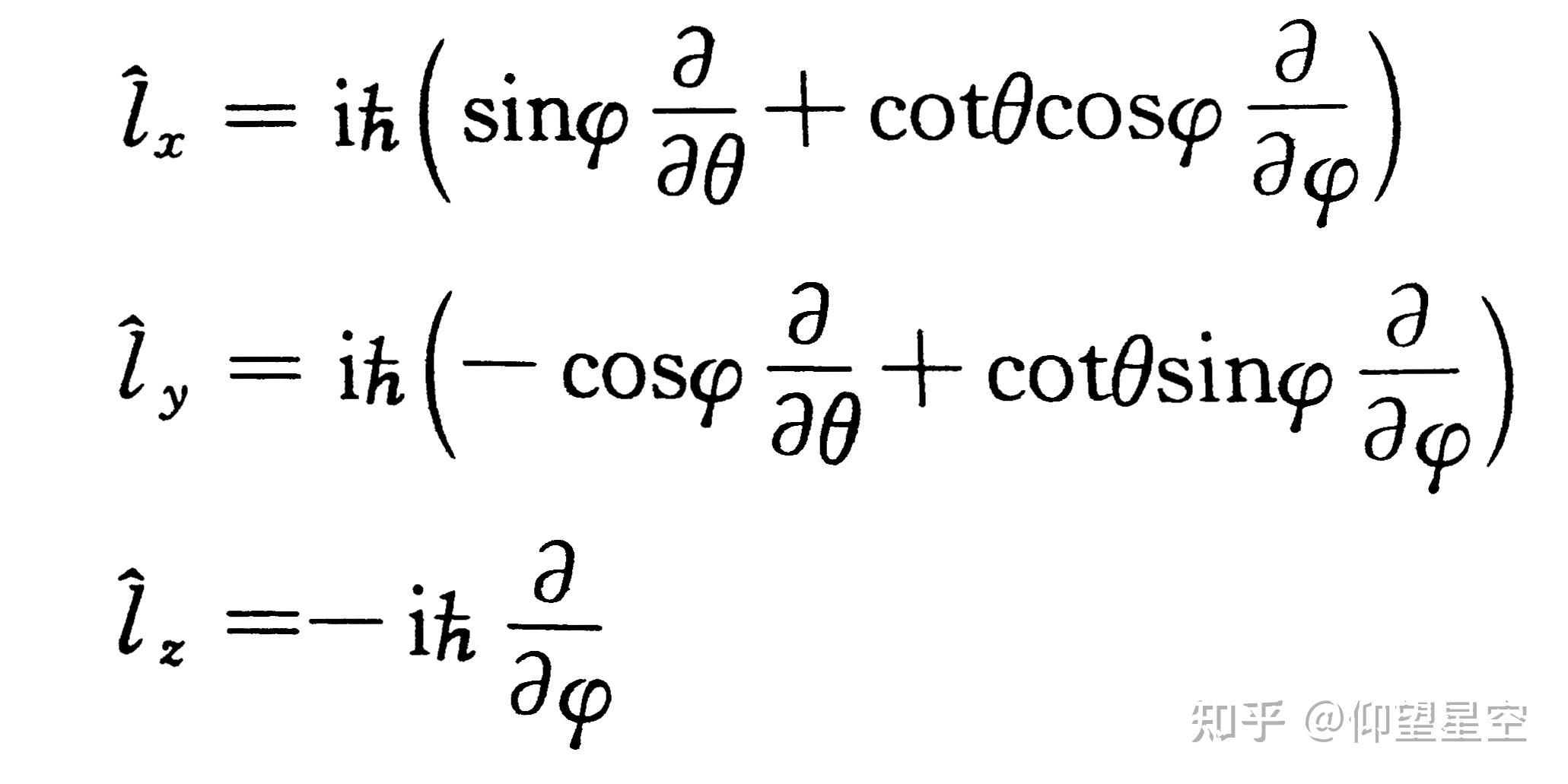 图片来源:维基百科
图片来源:维基百科
 图片来源:知乎专栏
图片来源:知乎专栏
这些图片展示了本征函数和本征值问题在数学和物理学中的应用,以及它们在量子力学中的重要性。
继续提问
相关问题
PH0的溶液可能有哪些,是酸性最强的溶液吗
请比较react native和Ionic在上手难易程度,多平台支持,插件丰富性,文档支持等方面的不同,然后打分推荐
请对RocketMQ和Kafka的吞吐量,稳定性,可扩展性,安装配置便利性,推送模式等方面进行比较,然后打分推荐
荷兰有哪些重要城市
奥利金为何认为上帝不能强迫灵魂回归?
為什麼1891年發行的香港開埠50周年紀念郵票引發了衝突?
动画电影《深海》的中国大陆票房成绩是多少?
谁在《美国队长:复仇者先锋》中扮演红骷髅?
什么是一手史料和二手史料,它们在历史研究中有何不同作用?
9·11事件后,阿拉伯裔和穆斯林美国人如何应对日益增加的仇恨犯罪和政府针对性措施?