参考资料
Moonshot回答
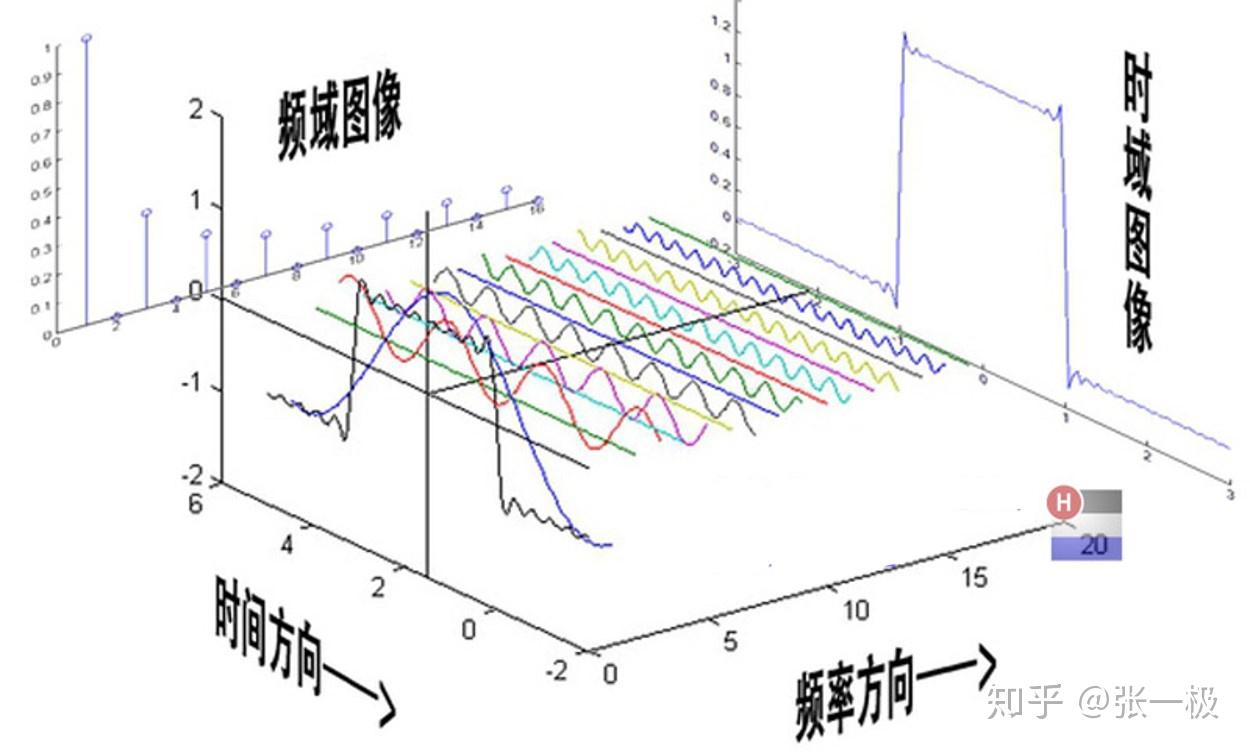
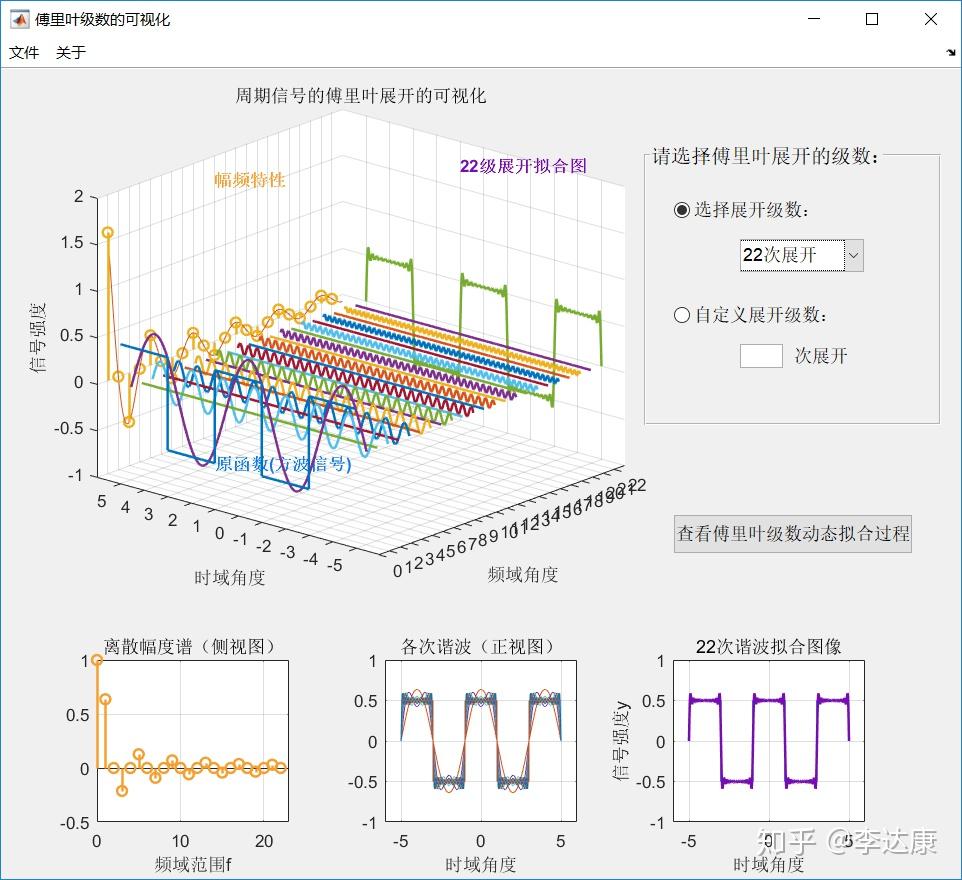
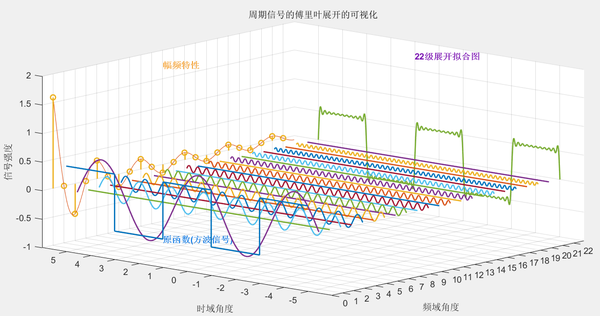
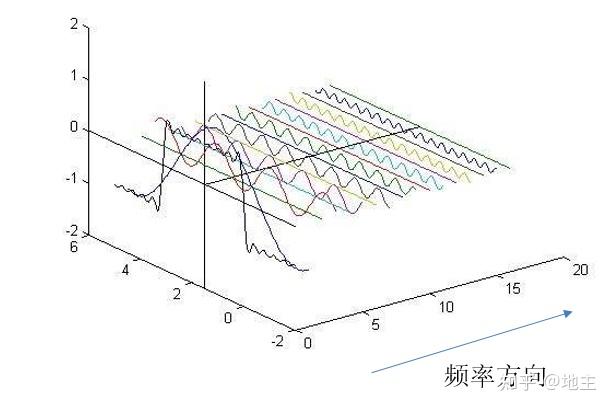
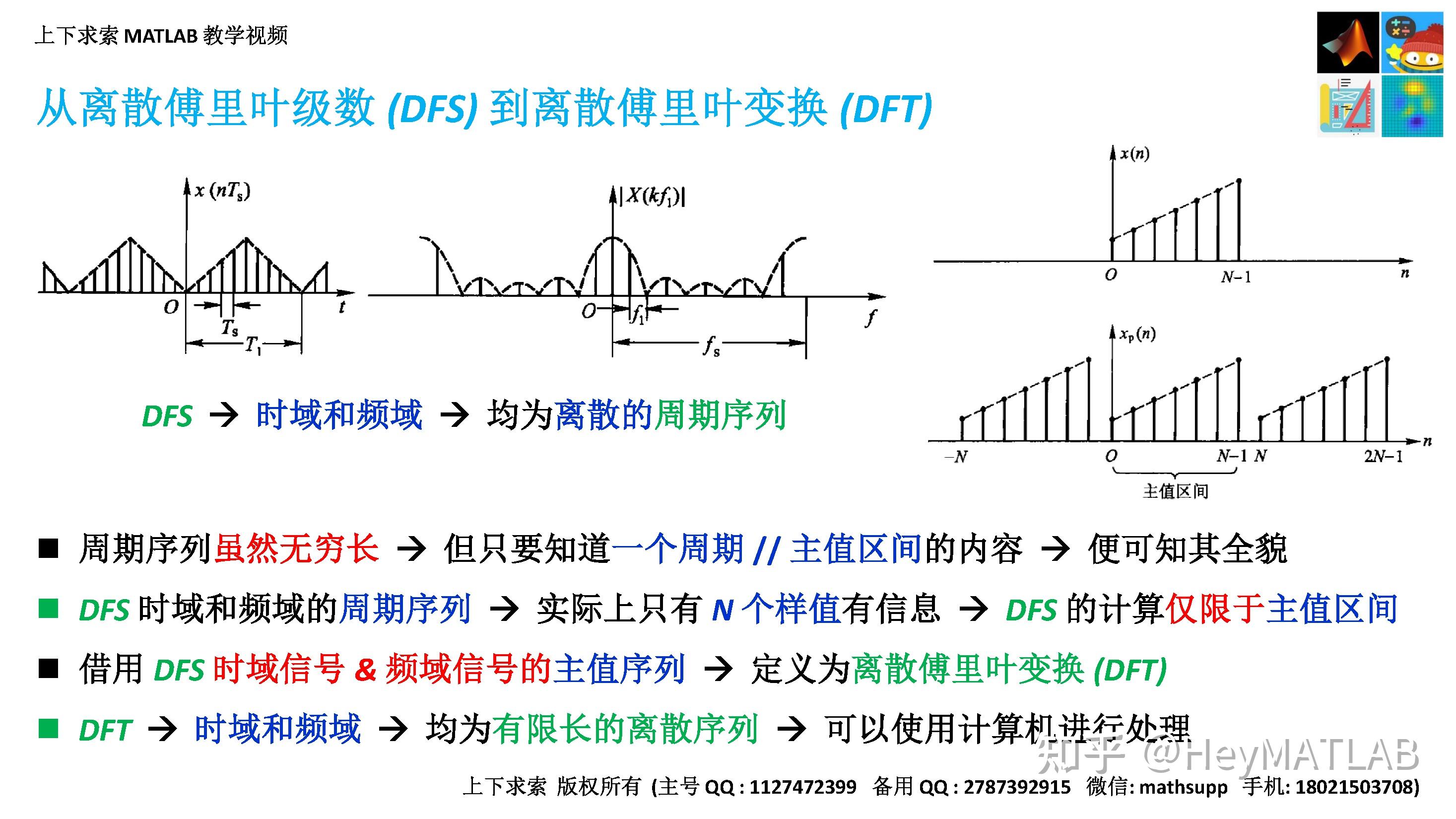
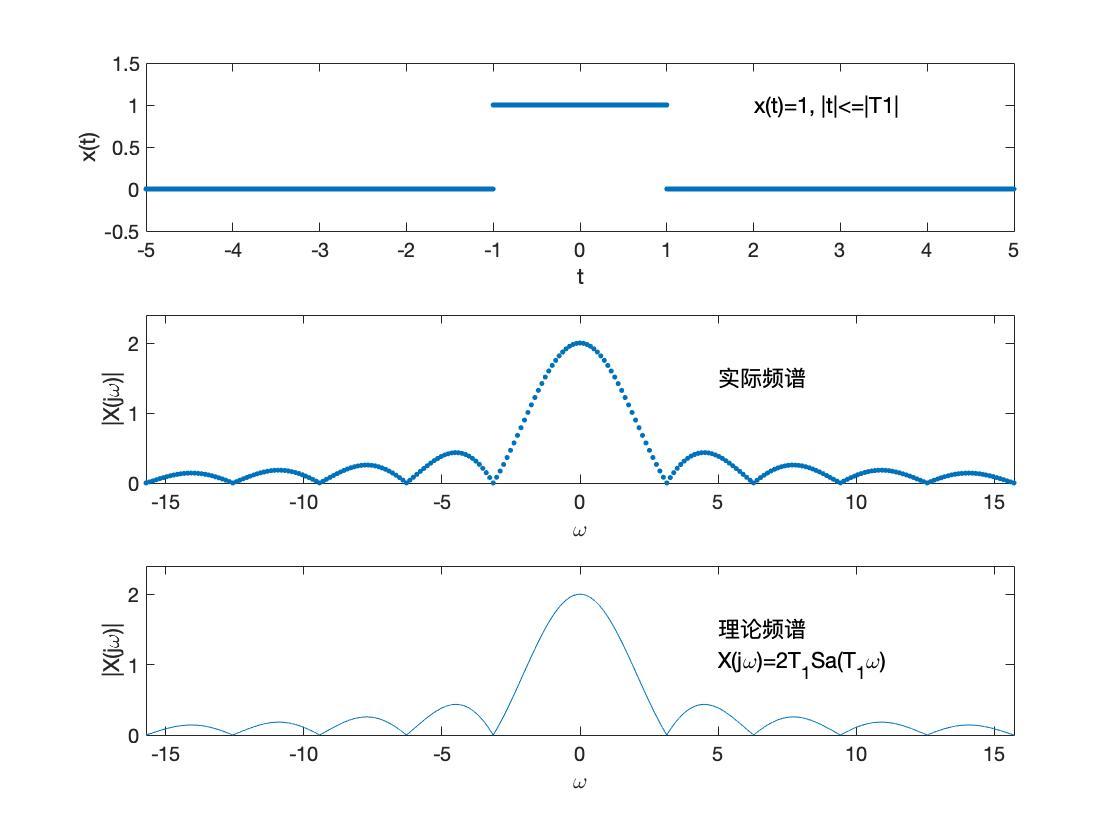
傅里叶分析的基本原理是将一个复杂的周期函数或信号分解为若干个简单的正弦波(或余弦波)的和。这一原理基于傅里叶级数和傅里叶变换的概念,其中傅里叶级数用于描述周期函数,而傅里叶变换则推广到非周期函数。通过这种分解,我们可以将复杂的信号转换到频域进行分析,从而更深入地理解信号的本质和特点。
傅里叶分析在工程和科学中有着广泛的应用,包括但不限于以下几个领域:
-
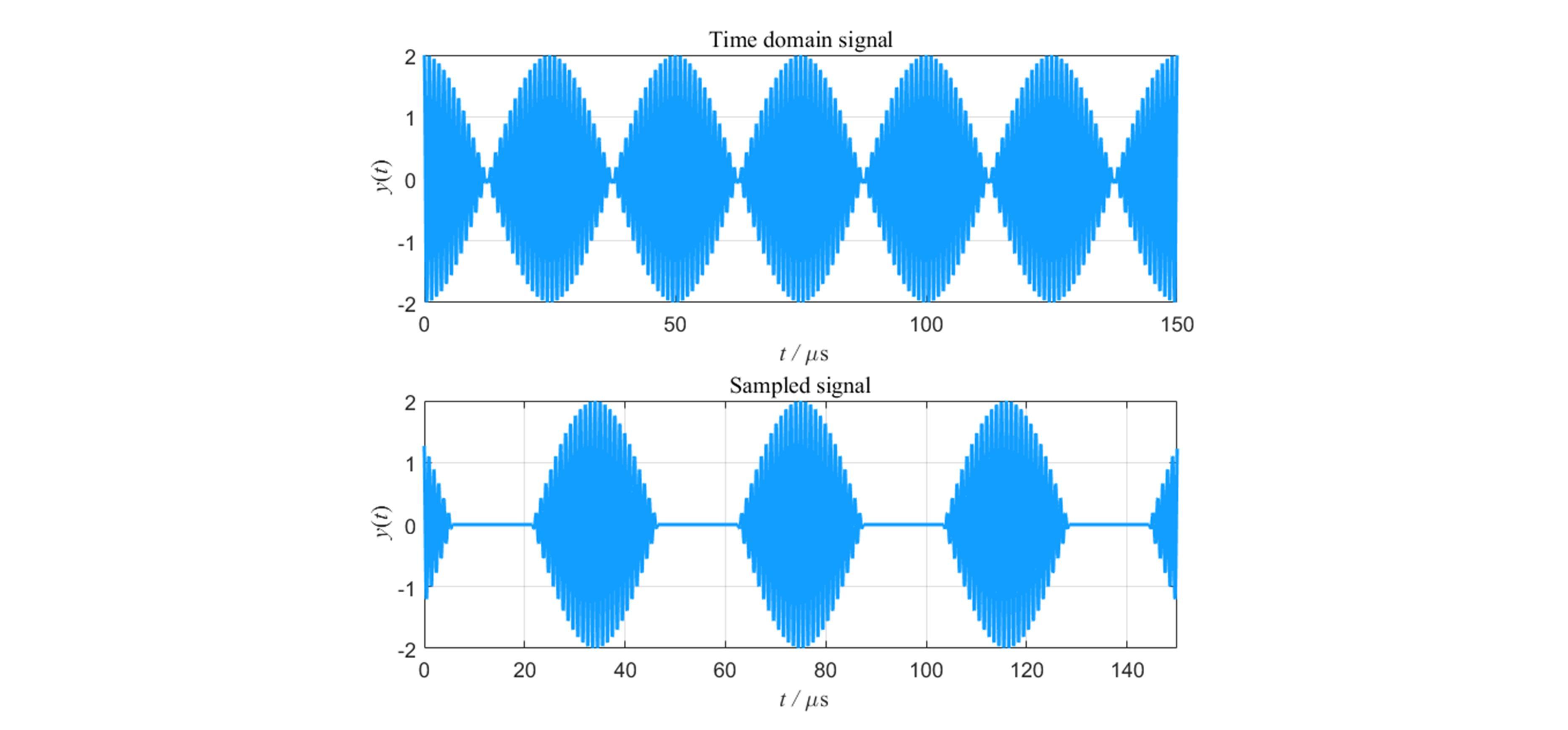
信号处理:在信号去噪、数据压缩和信号的频谱分析中,傅里叶变换被用来将时域信号转换为频域信号,以便更容易地分析和处理。例如,通过分析频谱,可以识别和滤除不需要的噪声成分。
-
图像处理:在图像处理中,傅里叶变换用于图像的频域滤波,如低通滤波器去除图像的高频噪声,或高通滤波器增强边缘等细节。
-
通信系统:在通信领域,傅里叶变换用于分析和设计滤波器、调制解调技术,以及多路复用技术等。
-
光谱分析:傅里叶变换在光谱学中用于分析物质的组成,通过物质对不同波长的光的吸收或发射特性,可以确定物质的成分。
-
地震学:在地震学中,傅里叶分析用于分析地震波,帮助地质学家理解地球内部的结构。
-
热传导和量子物理:在热传导问题中,傅里叶分析用于求解热传导方程,而在量子物理中,它用于分析波函数。
通过搜索结果,我们可以看到傅里叶分析在各个领域的应用实例,如图像处理中的降噪和锐化、物联网云计算中的频谱分析等。此外,还有许多教材和资源可以帮助深入学习傅里叶分析的原理和应用,例如《深入浅出傅里叶变换》和《傅里叶分析笔记》等。这些资源不仅提供了理论知识,还包括实际应用和示例,有助于更好地理解和掌握傅里叶分析。
继续提问
相关问题
蒙古军在莱格尼察战役后为何没有继续占领波兰?
彼岸岛的主要反派角色有哪些,他们有什么样的能力和目标?
在《蝙蝠侠:煤气灯下的哥谭》中,布鲁斯·韦恩的配音演员是谁?
为什么Credit Suisse对于DigitalOcean和Fastly的未来表现持中立态度?他们的核心理由是什么?
苏联在科技和艺术领域的发展受到了哪些批评?
托马斯·潘恩在《常识》中如何看待英王和英国议会的统治?
赤壁之战中,孙刘联军是如何利用火攻大败曹操的?
艾米莉·布朗特在《鱼跃奇缘》中饰演的角色名称是什么,这部电影的主要情节是什么?
金马奖历史上最年轻的获奖女演员是谁,她是在第几届金马奖中获奖的?
杜袭为何在荆州时拒绝辅佐刘表,认为他不是拨乱之主?