参考资料
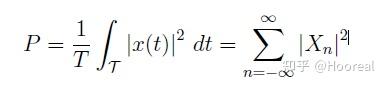
参考资料
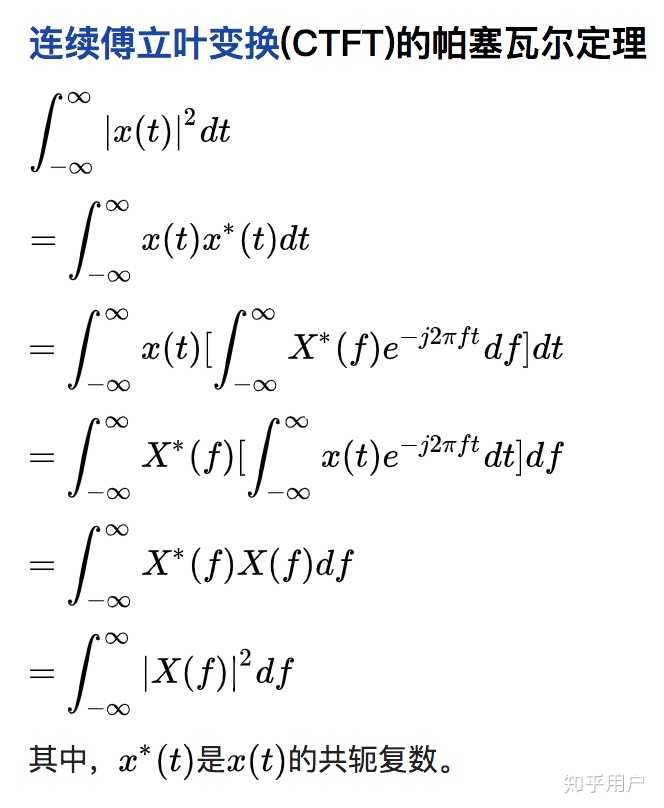
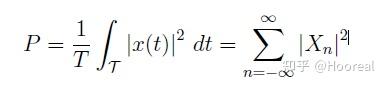
Moonshot回答
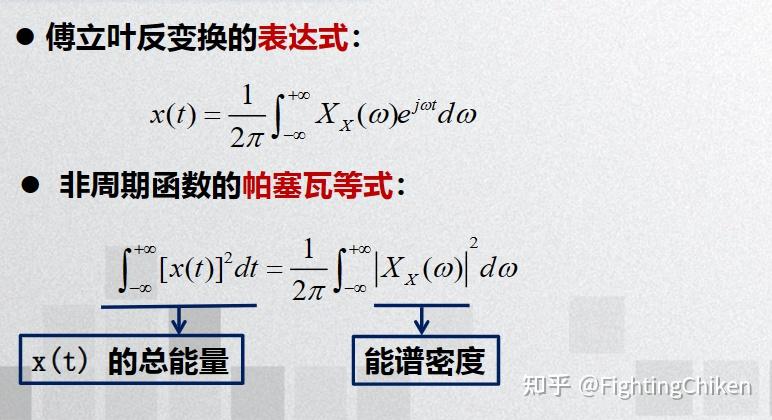
帕塞瓦尔定理，也称为帕塞瓦尔等式，是数学中的一个基本定理，它表明在傅里叶变换中，函数平方的和（或积分）等于其傅里叶变换式平方之和（或积分）。具体来说，对于一个函数( f(t) )，其在时域的能量与其在频域的能量是相等的，可以表示为：
[ \int_{-\infty}^{+\infty} |f(t)|^2 dt = \int_{-\infty}^{+\infty} |F(\omega)|^2 d\omega ]
其中，( F(\omega) )是( f(t) )的傅里叶变换。
在能量和功率谱密度的计算中，帕塞瓦尔定理有着重要的应用。对于能量信号，其总能量是有限的，帕塞瓦尔定理可以用来计算信号在频域的能量分布，即能量谱密度。能量谱密度是指单位频带内的能量，通过傅里叶变换可以求得信号的能量谱密度，进而分析信号的频域特性。
对于功率信号，其功率是有限而非能量，帕塞瓦尔定理可以用来计算信号的功率谱密度。功率谱密度是指单位频带内的功率，通过傅里叶变换可以求得信号的功率谱密度，进而分析信号的功率如何在频域分布。
在实际应用中，例如在通信系统中，帕塞瓦尔定理可以帮助我们计算信号的总功率，进而分析信噪比、设计滤波器等。此外，功率谱密度的概念在分析随机信号时也非常重要，它有助于我们理解信号的统计特性。
通过搜索结果，我们可以看到帕塞瓦尔定理在功率谱和能量谱的计算中扮演着核心角色。例如，在知乎专栏的文章《今天，从头捋一捋功率谱和能量谱》中提到，帕塞瓦尔定理指的是时域和频域内能量是守恒的，可以借助能量密度的概念来理解频域中的能量分布情况。而在《随机信号的功率谱密度究竟有什么物理意义？》中提到，根据帕塞瓦尔定理，信号的能量可以转换为频域中的分布情况，从而计算功率谱密度。这些信息进一步证实了帕塞瓦尔定理在能量和功率谱密度计算中的重要性。