参考资料



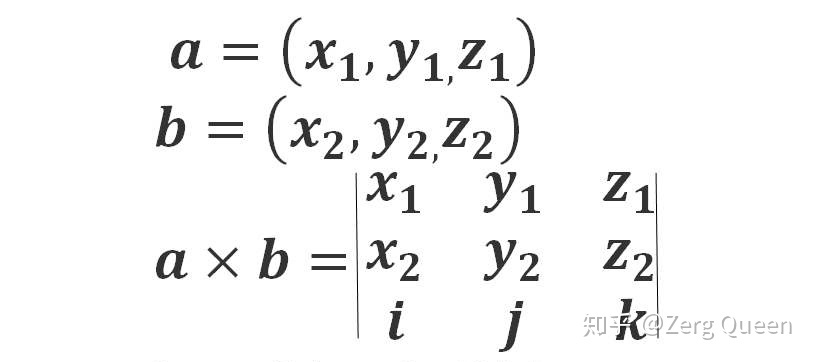
参考资料
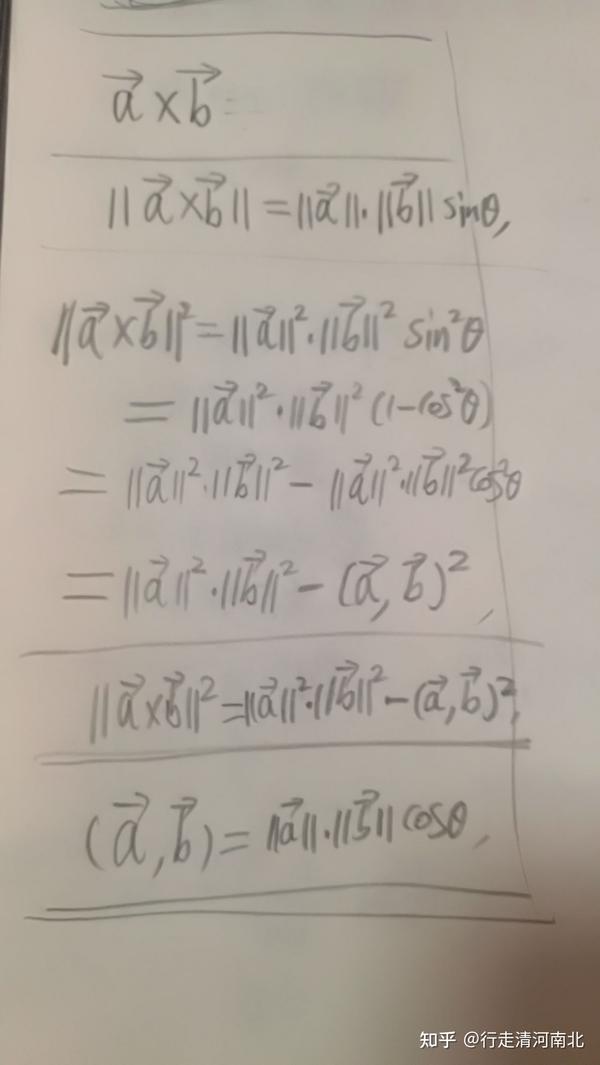

Moonshot回答
向量的外积(又称为叉积或楔积)的规范数(模长)计算公式是:
[ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin(\theta) ]
其中,(|\mathbf{a}|) 和 (|\mathbf{b}|) 分别是向量 (\mathbf{a}) 和 (\mathbf{b}) 的模长,(\theta) 是两个向量之间的夹角。
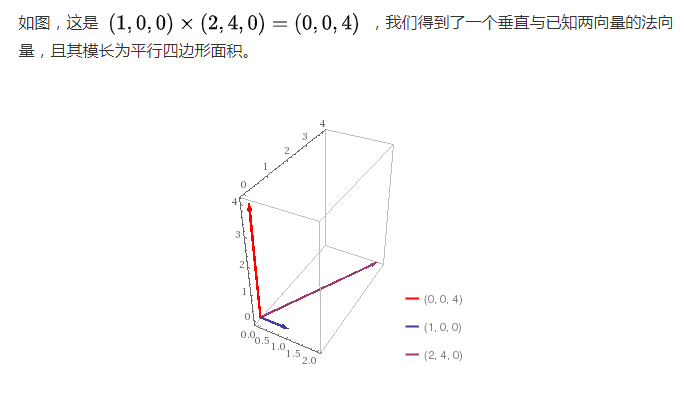
外积的模长与两个向量的模长和它们之间的夹角有直接关系。具体来说,外积的模长等于两个向量模长的乘积与它们夹角的正弦值。这意味着当两个向量之间的夹角为90度时(即正弦值为1),外积的模长达到最大,此时外积的模长等于两个向量模长的乘积。这反映了两个向量在空间中张成的平行四边形的面积。
 图片来源:CSDN
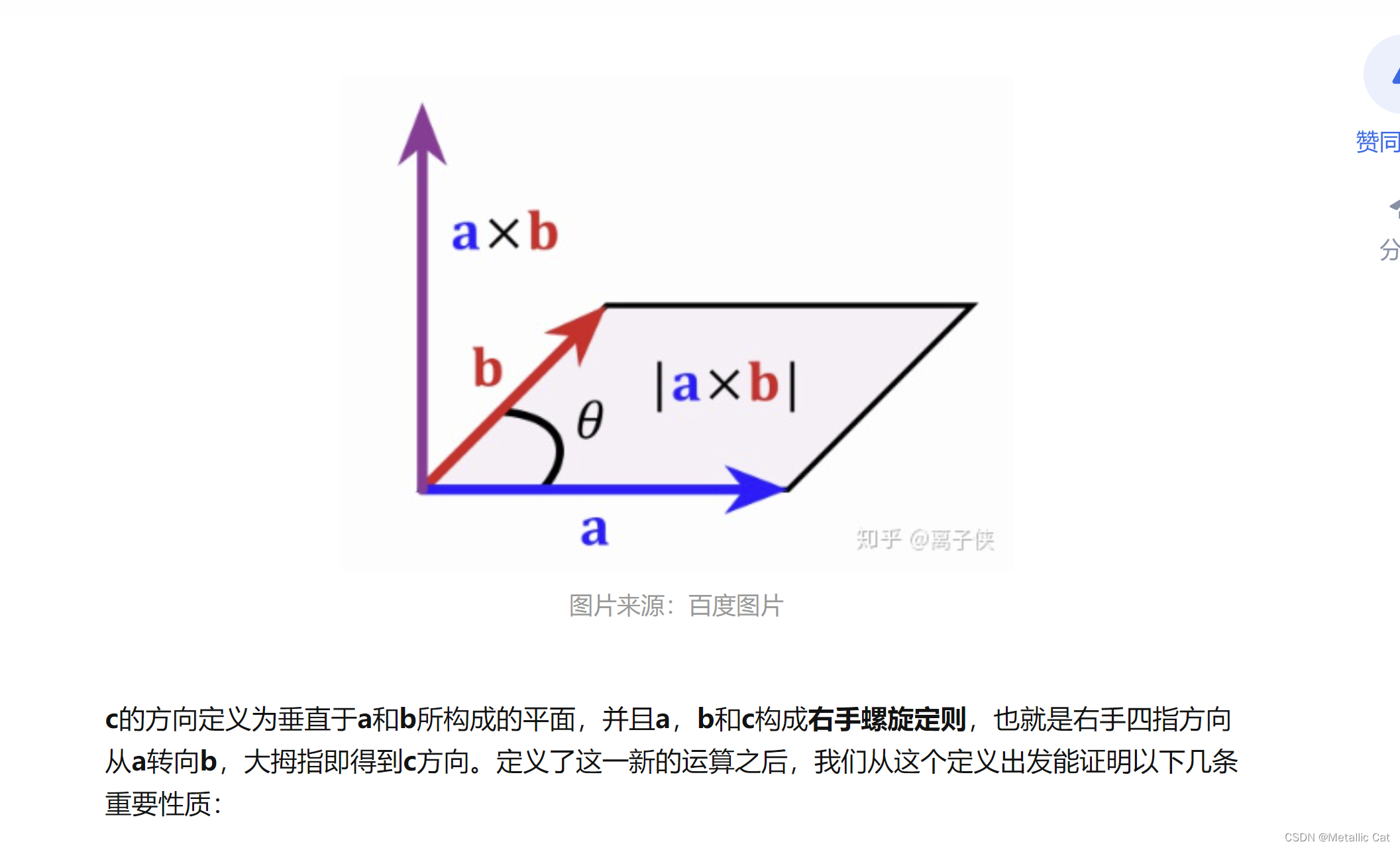
图片来源:CSDN
此外,外积的方向遵循右手定则,即如果你的右手的四指从第一个向量 (\mathbf{a}) 以最短角度旋转到第二个向量 (\mathbf{b}),那么你的拇指指向的方向就是外积向量的方向。如果两个向量平行(夹角为0度或180度),它们的外积为零向量,因为正弦值为0。
继续提问
相关问题
在美股市场上,标普500、道琼斯工业指数和纳斯达克指数的市盈率和市净率分别处于什么样的水平,是否表明当前美股估值存在下调压力?
2013年发行的《幻影车神3》电影的高潮场景在哪里拍摄,这个场地还有什么著名的电影使用过?
为什么珍妮弗·奥马选择使用轮转基金而不是传统银行进行储蓄和借款?
查理·马特作为宫相,为何在国王去世后不立新君,最终导致加洛林王朝的建立?
矶村俊在《名侦探柯南》中提供了什么样的帮助,他与谁是邻居关系?
解释电影《留住有情人》中的主角亚历山大试图通过怎样的方式来保持与芳芳的关系?
艾曼纽尔·卢贝茨基连续三次获得奥斯卡最佳摄影奖,他分别凭借哪三部电影获奖?
《东京家族》电影由哪位日本导演执导,最初在哪一年上映的?
大永年间,哪位室町幕府将军去世?
川崎在各地区分公司的位置和联系方式是什么,在不同地区的销售和服务有什么差异?