参考资料
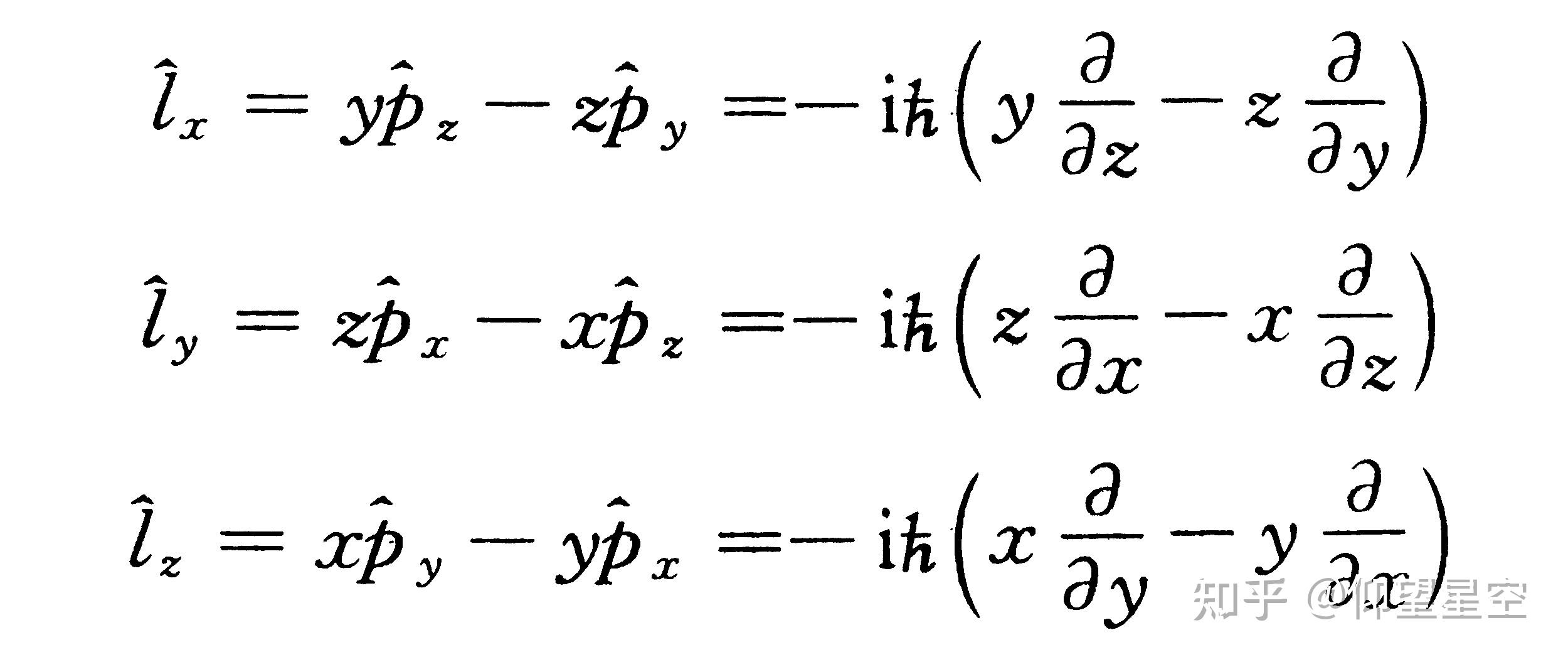
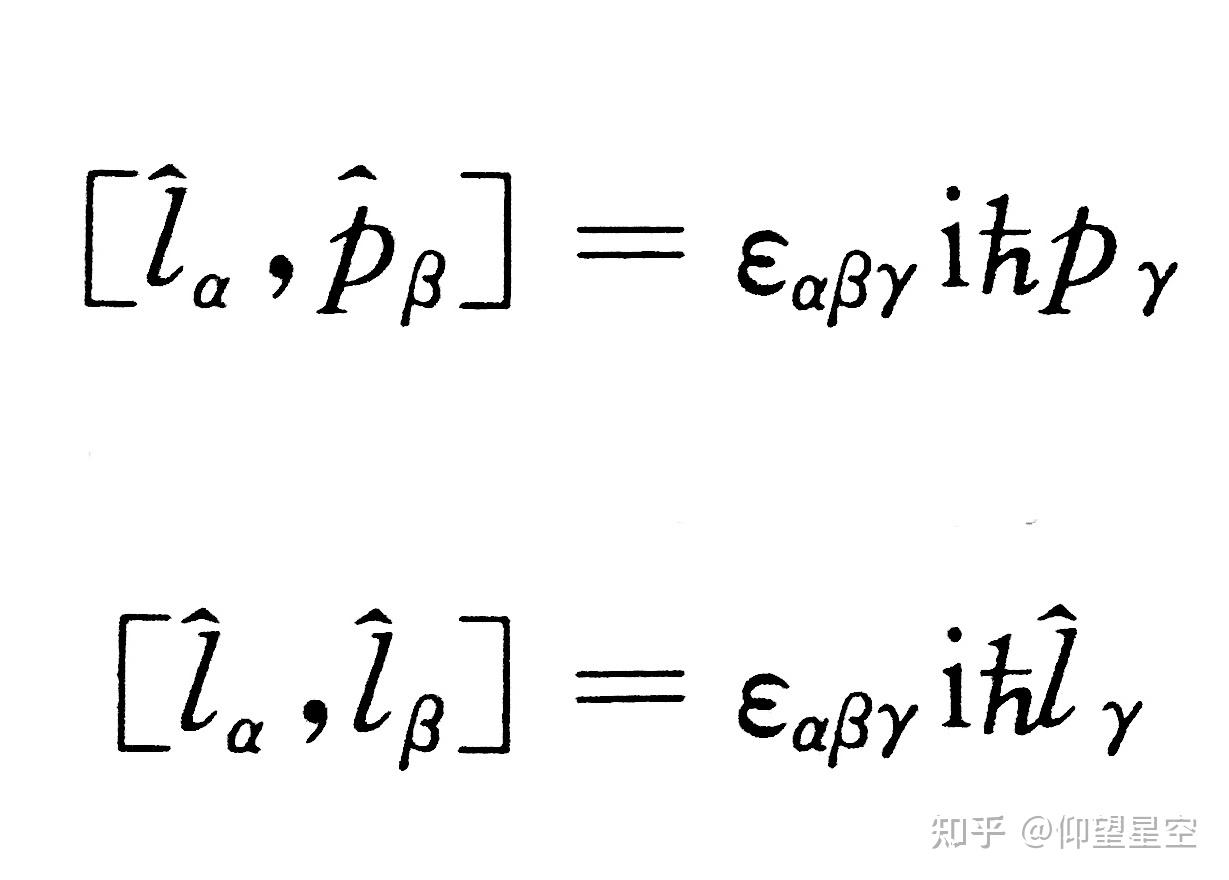
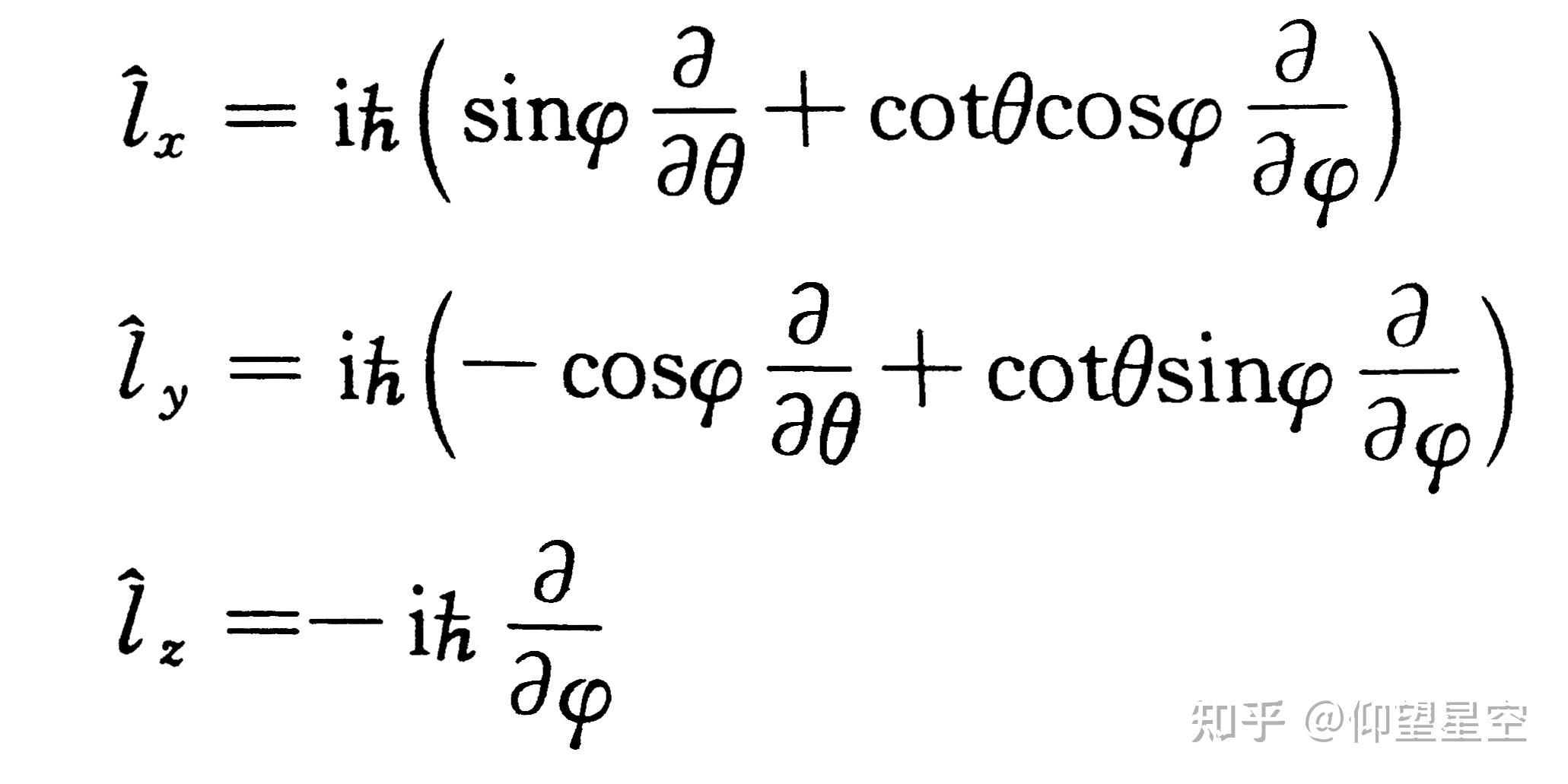

参考资料


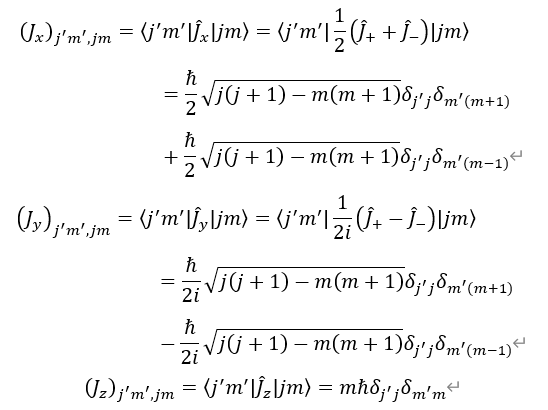
Moonshot回答
在量子力学中,总角动量算符是轨道角动量算符((\vec{L}))和自旋角动量算符((\vec{S}))的矢量和,表示为 (\vec{J} = \vec{L} + \vec{S})。这一概念在量子力学的多个领域中都有重要应用。
-
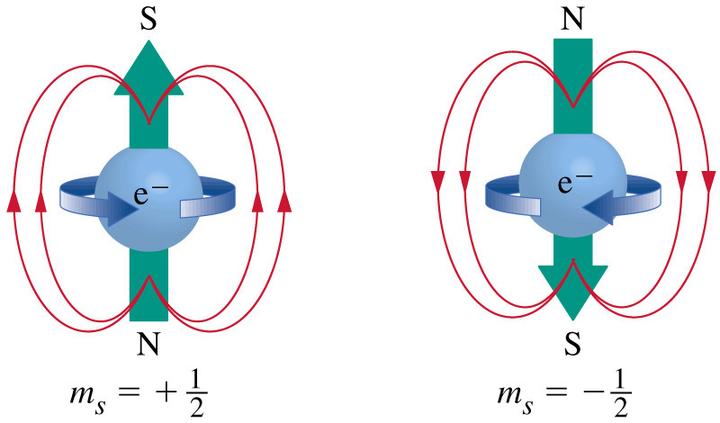
角动量的加总:根据量子力学的规则,两个角动量(无论是轨道角动量还是自旋角动量)可以通过它们的分量进行矢量加总。这意味着对于一个给定的系统,我们可以将自旋角动量和轨道角动量相加,得到总角动量。这种加总遵循量子力学的角动量叠加原理,其中角动量的各个分量(如 (L_x), (L_y), (L_z) 对于轨道角动量,和 (S_x), (S_y), (S_z) 对于自旋角动量)满足特定的对易关系。
-
量子力学应用:总角动量算符在量子力学中有着广泛的应用。例如,在描述原子中电子的行为时,总角动量是守恒量,这意味着在没有外力作用的情况下,原子的总角动量不会改变。这一性质对于解释原子的光谱线和电子的能级非常重要。此外,总角动量的概念也在描述粒子的磁矩、粒子的统计性质(如玻色子和费米子的行为)以及粒子的衰变过程等方面发挥作用。
从搜索结果中,我们可以看到量子力学中角动量的普遍性质,包括角动量算符与旋转算符的联系,以及角动量守恒的概念。此外,总角动量量子数是描述粒子总角动量的一个重要参数,它由轨道角动量量子数((\ell))和自旋量子数((s))共同决定。这些信息进一步强调了总角动量算符在量子力学中的重要性和应用范围。
继续提问
相关问题
阿什凯隆在1950年代是如何从一个阿拉伯城镇转变为现代城市的?
安哈尔特公国是如何在1863年重新统一的?
在文化基因和价值传承方面,企业如何能够建立长久的成功机制以避免短命的危机?
黑死病对欧洲社会产生了哪些深远的影响?它如何改变了欧洲的社会结构和宗教信仰?
《地狱天使》漫画总共有几本单行本,分别是在什么时间发行的?
海顿·格温在《温莎王朝》中饰演卡米拉的表演与她以往的角色相比有什么不同吗?
电影《闪灵》中标志性场景有哪几个,这些场景在原著小说中是否存在?
杜袭在汉中之战中如何成功安定军心,替代夏侯渊的位置?
《知否知否应是绿肥红瘦》在2019年上海电视节白玉兰奖中获得了哪些提名?
西夏的艺术文化有哪些独特的表现形式?