外代数中的楔积与叉积在数学上有什么区别,楔积如何用于定义角动量?
参考资料
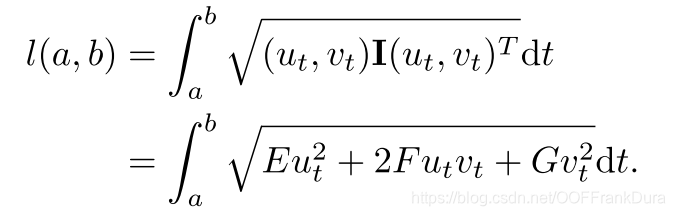
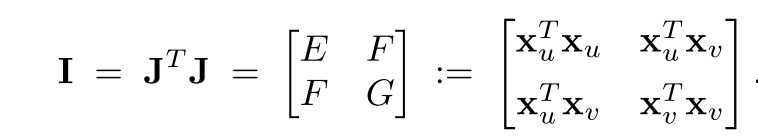
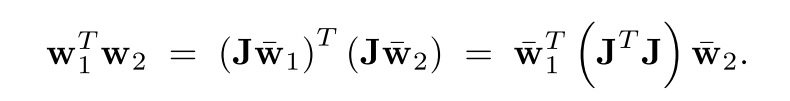
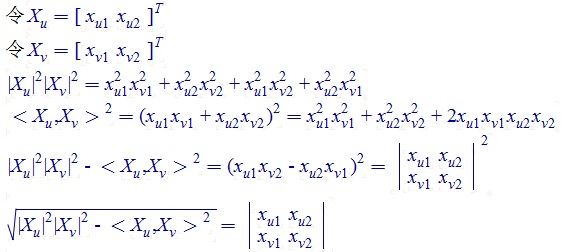
参考资料
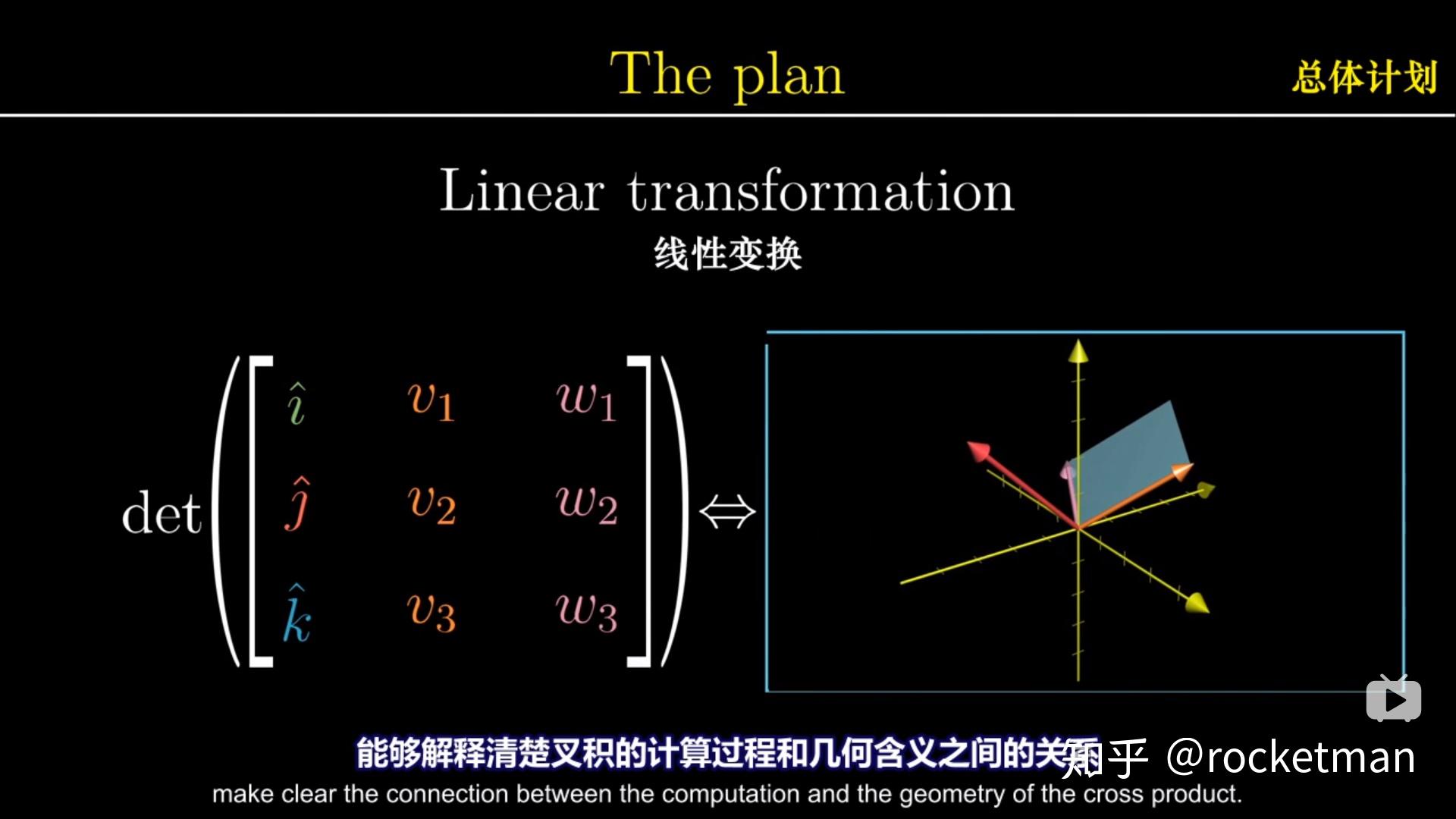

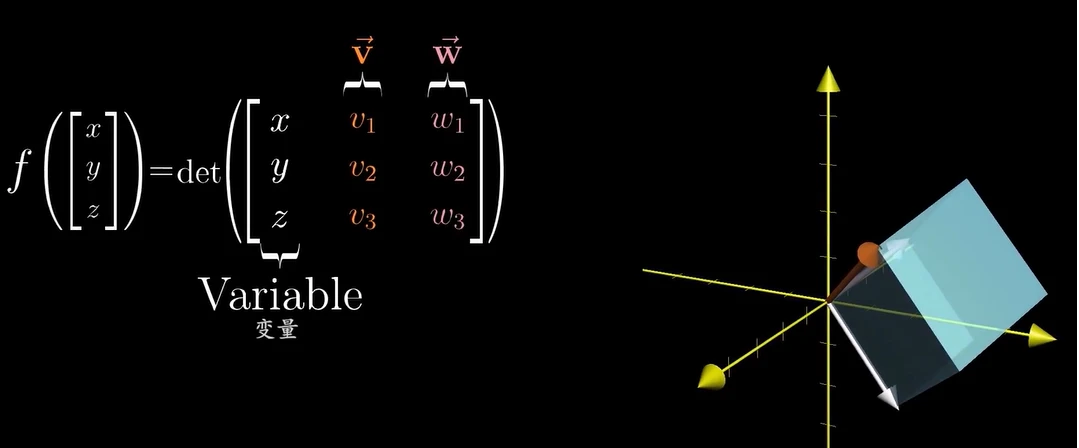

参考资料
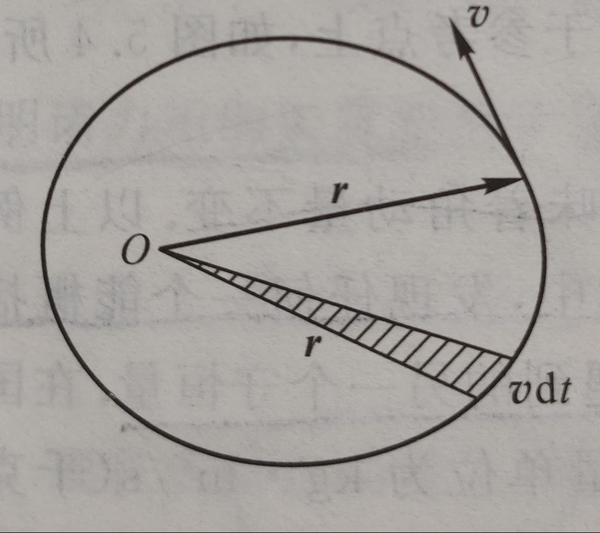
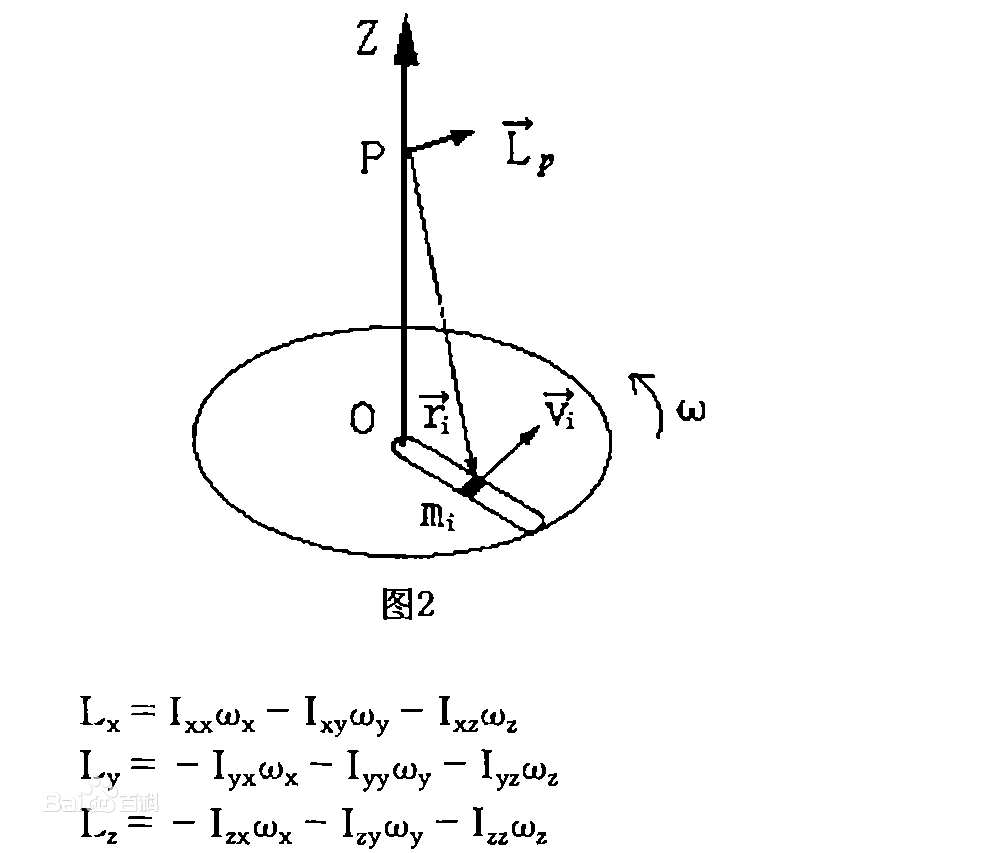
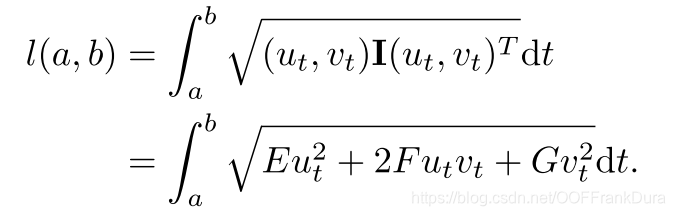

Moonshot回答
在数学中,楔积和叉积是两种不同的运算,它们在代数结构和应用上有显著的区别。
楔积是一种在外代数中定义的操作,它具有反对称性和双线性。楔积的结果是一个新的向量,称为外积或楔积,它反映了两个向量之间的有向面积。楔积在多维空间中定义,不仅限于三维,并且可以作用于任意数量的向量。楔积的一个关键性质是其反对称性,即交换两个向量的顺序会改变结果的符号。此外,楔积还具有结合性,这使得它可以扩展到多个向量的乘积。在物理学中,楔积用于定义角动量。在经典力学中,角动量是位置向量和动量向量的叉积。在相对论力学中,角动量可以表示为一个逆变二阶反对称张量,其分量可以通过楔积来定义。这种表示方法可以推广到更高维度的空间,并且能够更自然地处理角动量的变换性质。
叉积,又称为向量积,是三维空间中两个向量的一种特殊乘积。叉积的结果是一个垂直于两个原始向量所定义平面的向量,其大小等于两个向量构成的平行四边形的面积,方向遵循右手定则。叉积不具有结合性,并且仅在三维空间中有定义。叉积通常用于计算力矩和角动量,例如在物理学中,一个物体绕轴的角动量可以表示为位置向量和动量向量的叉积。
总的来说,楔积是一种更为一般的概念,适用于多维空间,而叉积是楔积在三维空间中的一个特例。在物理学中,楔积提供了一种更为普适和协变的方法来定义和处理角动量等物理量。