参考资料

在流体动力学中，玻尔兹曼方程与温度和压力的关联可以通过以下方式理解：

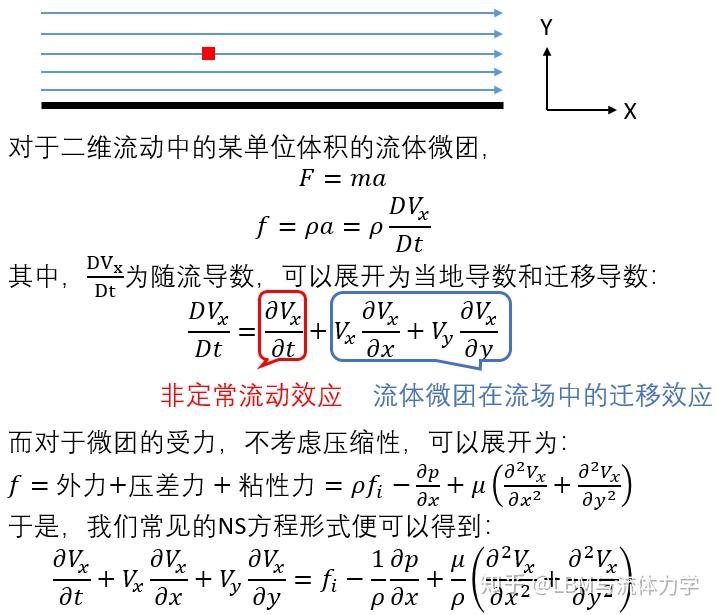
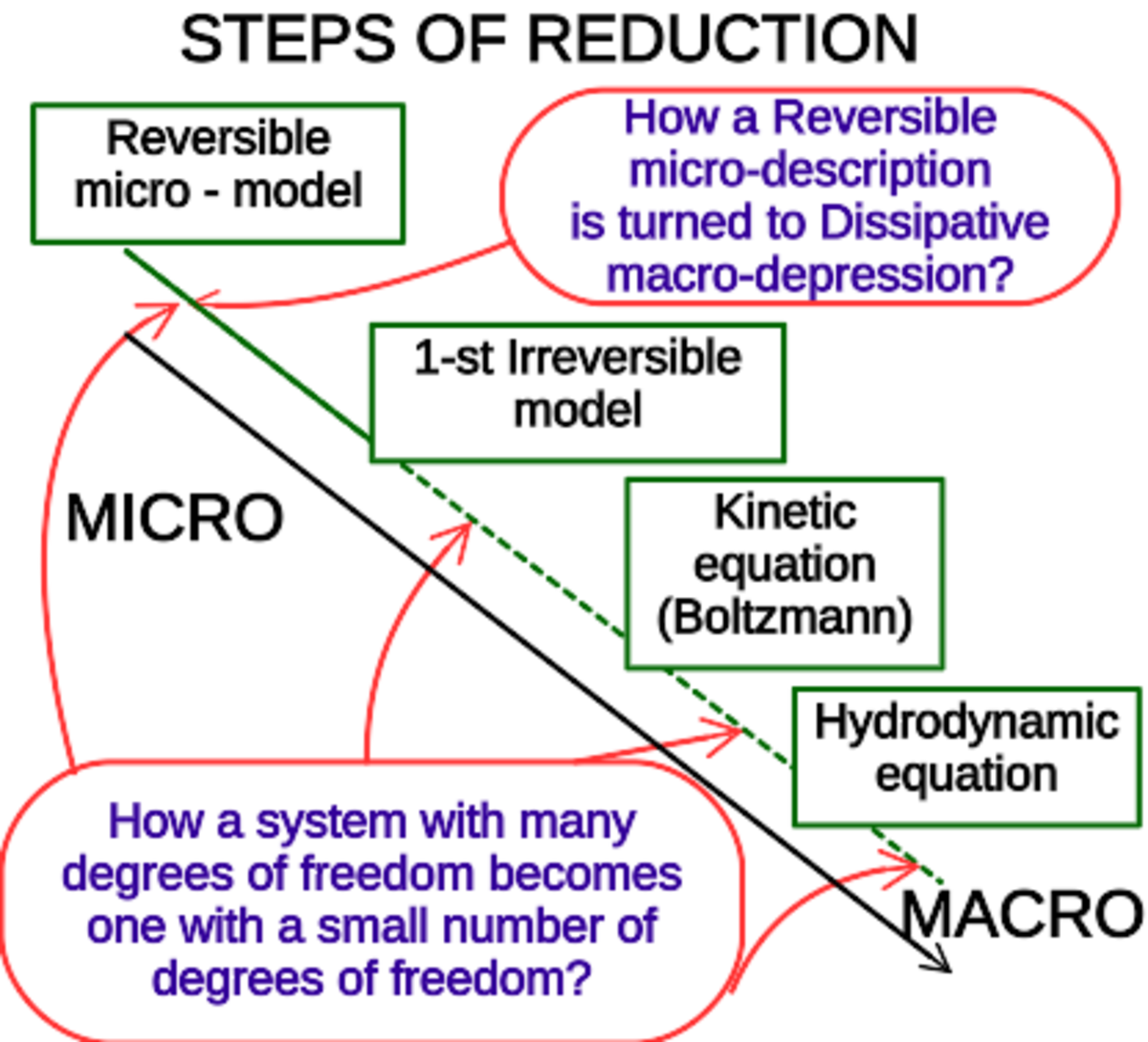
1. 从微观到宏观的过渡：玻尔兹曼方程描述了粒子分布函数随时间的演化，这个方程可以被用来推导出宏观的流体动力学方程，包括连续性方程、动量方程和能量方程。这些方程描述了流体的密度、速度和温度场随时间的变化。

2. 局域平衡假设：在流体动力学中，我们通常假设系统处于局域平衡态，这意味着在每一个空间点，流体的宏观量（如密度、速度和温度）可以被定义，并且它们满足宏观的流体动力学方程。

3. 温度和压力的宏观定义：在流体动力学中，温度和压力是宏观量，它们可以通过局域平衡假设与玻尔兹曼方程联系起来。例如，温度可以通过能量分布来定义，而压力可以通过动量的输运来定义。

4. 输运系数：在从玻尔兹曼方程到流体动力学方程的推导过程中，会出现一些输运系数，如粘性系数和热导率。这些系数将宏观的物理量（如压力梯度和温度梯度）与流体的输运过程（如粘性应力和热流）联系起来。

5. 弛豫时间：玻尔兹曼方程中引入了弛豫时间的概念，这是系统从非平衡状态恢复到平衡状态所需的时间尺度。在流体动力学中，这个时间尺度通常远小于研究的时间尺度，因此可以假设系统处于局域平衡态。

通过搜索结果，我们可以看到，例如在知乎的讨论中提到了使用"玻尔兹曼方程，两项近似"接口来定义流体的物理属性，如粘性、压力和温度等。这些属性可能与组分的输运相关。此外，维基百科上关于玻尔兹曼方程的页面也提到了它在描述具有温度梯度的流体系统中的应用。这些信息进一步证实了玻尔兹曼方程与流体动力学中温度和压力的紧密联系。