分离变量法在解偏微分方程中是如何运用的,为什么它在扭曲几何中很有用?
参考资料
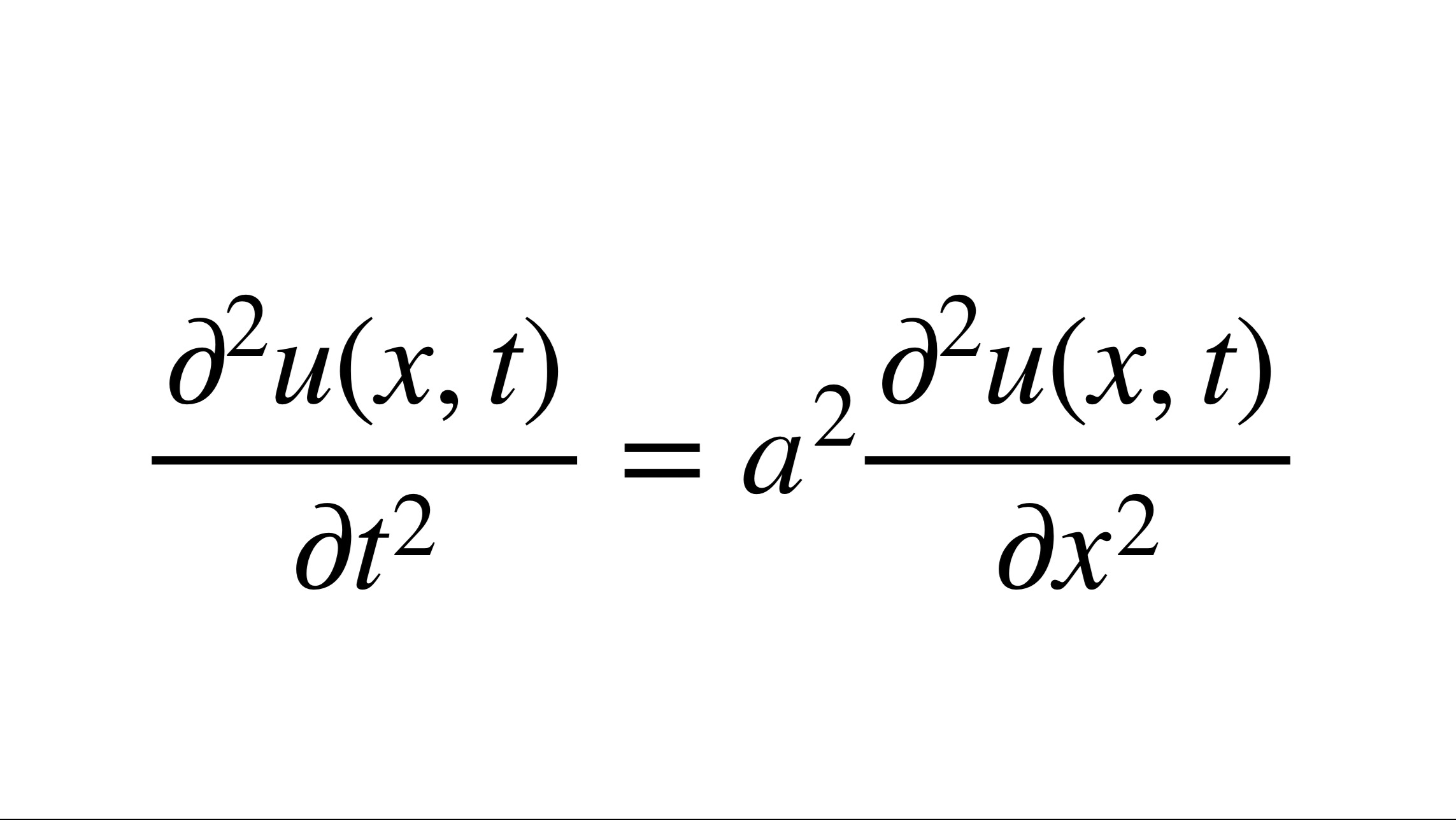



参考资料


Moonshot回答
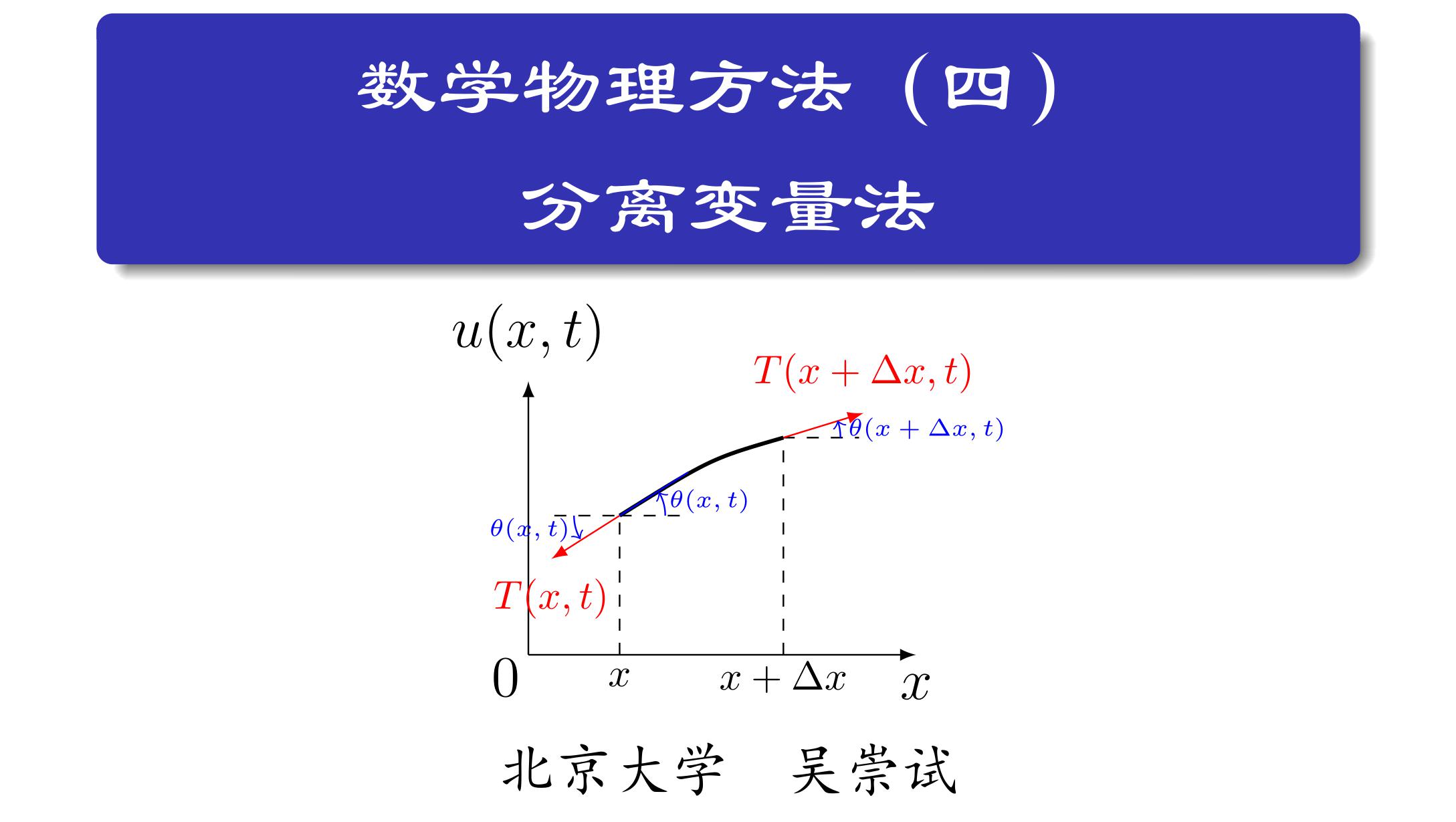
分离变量法是一种在解偏微分方程(PDEs)时常用的技术,它通过将多变量的PDE转化为一系列单变量的常微分方程(ODEs)来简化问题。这种方法特别适用于具有简单几何形状的区域,例如矩形、柱体或球体,因为这些区域的边界条件通常更容易处理。
在扭曲几何中,分离变量法之所以有用,是因为即使在复杂的几何形状中,如果方程的解可以表示为不同变量的函数的乘积,那么这种方法仍然可以应用。例如,在处理波动方程时,分离变量法可以揭示解的空间和时间部分,这有助于理解波动如何在复杂的空间结构中传播。
从搜索结果中,我们可以看到分离变量法在解偏微分方程中的应用。它通过将方程中的各个变量项分离,然后求解得到的常微分方程来找到PDE的解。这种方法依赖于线性叠加原理,将非齐次方程拆分为多个齐次或易于求解的方程。在扭曲几何中,这种方法有助于简化问题的复杂性,通过将问题分解为更小、更易于管理的部分来找到解决方案。
此外,分离变量法在数学物理中也是一种基本方法,它建立在叠加原理的基础上。这种方法不仅适用于简单的几何形状,也可以扩展到更复杂的扭曲几何中,只要解可以表示为不同变量的函数的乘积。
总的来说,分离变量法在扭曲几何中的有用性在于其能够将复杂的多维问题简化为一系列更简单的一维问题,从而降低了问题的复杂性并提供了求解的途径。这种方法的应用广泛,从基础的科学问题到工程和物理领域的实际问题都有其身影。