费米-狄拉克分布与玻色–爱因斯坦分布在物理学中的作用和区别是什么?
参考资料

参考资料


参考资料




Moonshot回答
费米-狄拉克分布和玻色-爱因斯坦分布是量子统计力学中描述粒子在不同能态上分布的两种基本方式。它们在物理学中扮演着重要的角色,并且具有明显的区别。
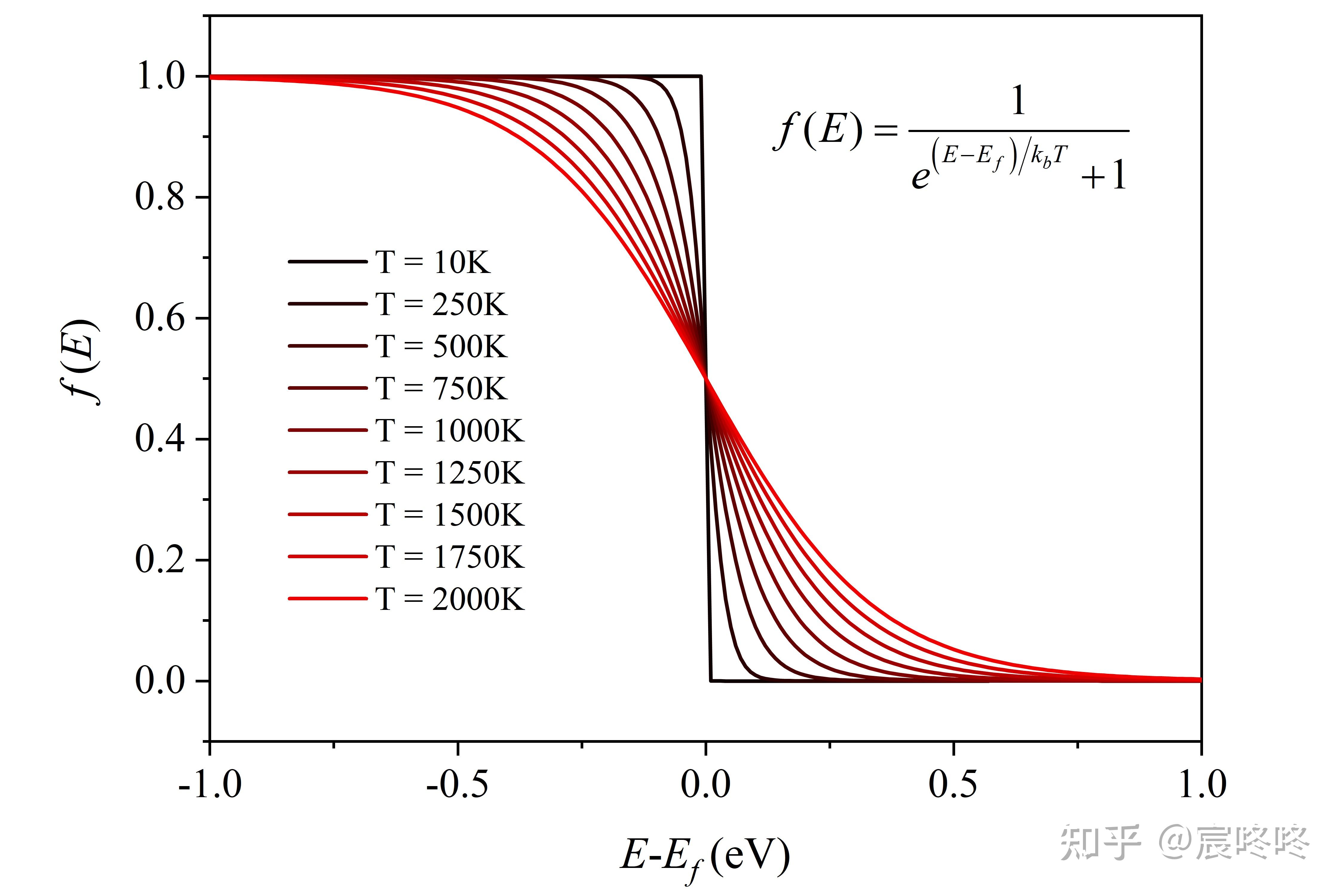
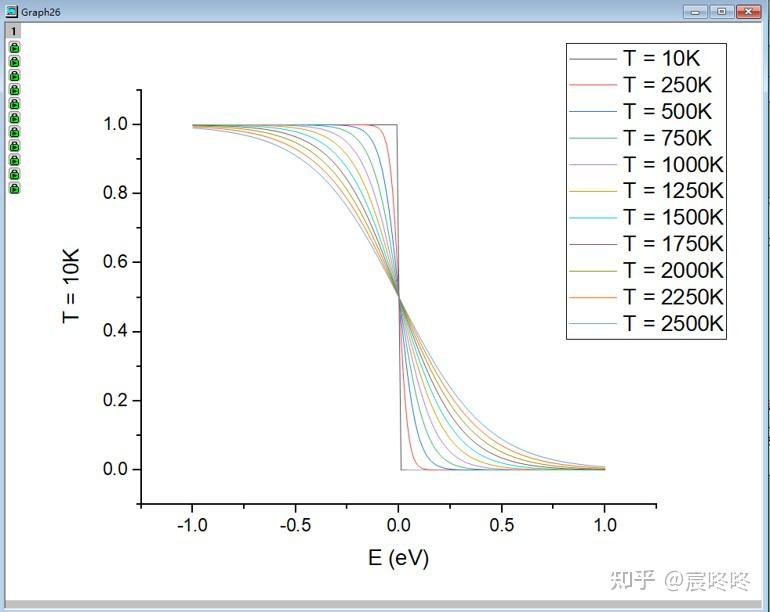
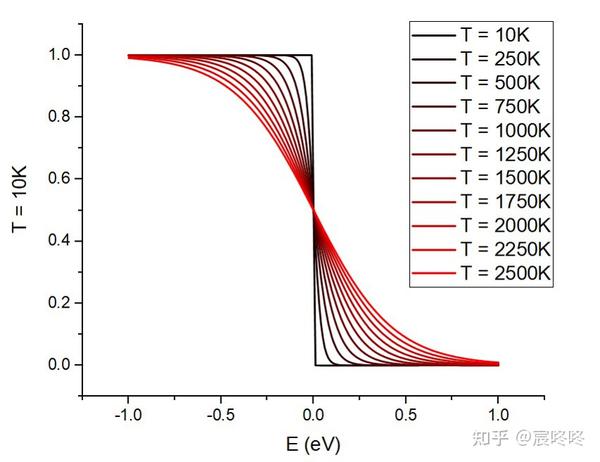
费米-狄拉克分布主要适用于费米子,即自旋为半整数的粒子(如电子、质子和中子)。这种分布体现了泡利不相容原理,即同一量子态不能被两个或更多的费米子同时占据。费米-狄拉克分布在描述电子在固体材料中的行为、金属和半导体的导电性、白矮星和中子星的物理性质等方面具有重要作用。例如,根据百度百科,“费米-狄拉克统计的适用对象是热平衡的费米子(自旋量子数为半奇数的粒子)”,并且“不同的粒子分处不同能态,这点对系统许多性质会产生影响”[1]。
玻色-爱因斯坦分布则适用于玻色子,即自旋为整数的粒子(如光子、声子和W/Z玻色子)。与费米子不同,多个玻色子可以占据同一量子态,这导致了玻色-爱因斯坦凝聚等现象。这种分布在解释黑体辐射、激光原理、超导性以及宇宙背景微波辐射等方面至关重要。维基百科中提到,“玻色子是自旋为整数的粒子,其本征波函数对称,在玻色子的某一个能级上,可以容纳无限个粒子”[2]。
两者的主要区别在于它们描述的粒子类型(费米子与玻色子)和统计性质。费米-狄拉克分布体现了泡利不相容原理,而玻色-爱因斯坦分布则允许粒子聚集在同一量子态。这些分布不仅在理论物理学中非常重要,而且在现代科技和工程应用中也扮演着关键角色。
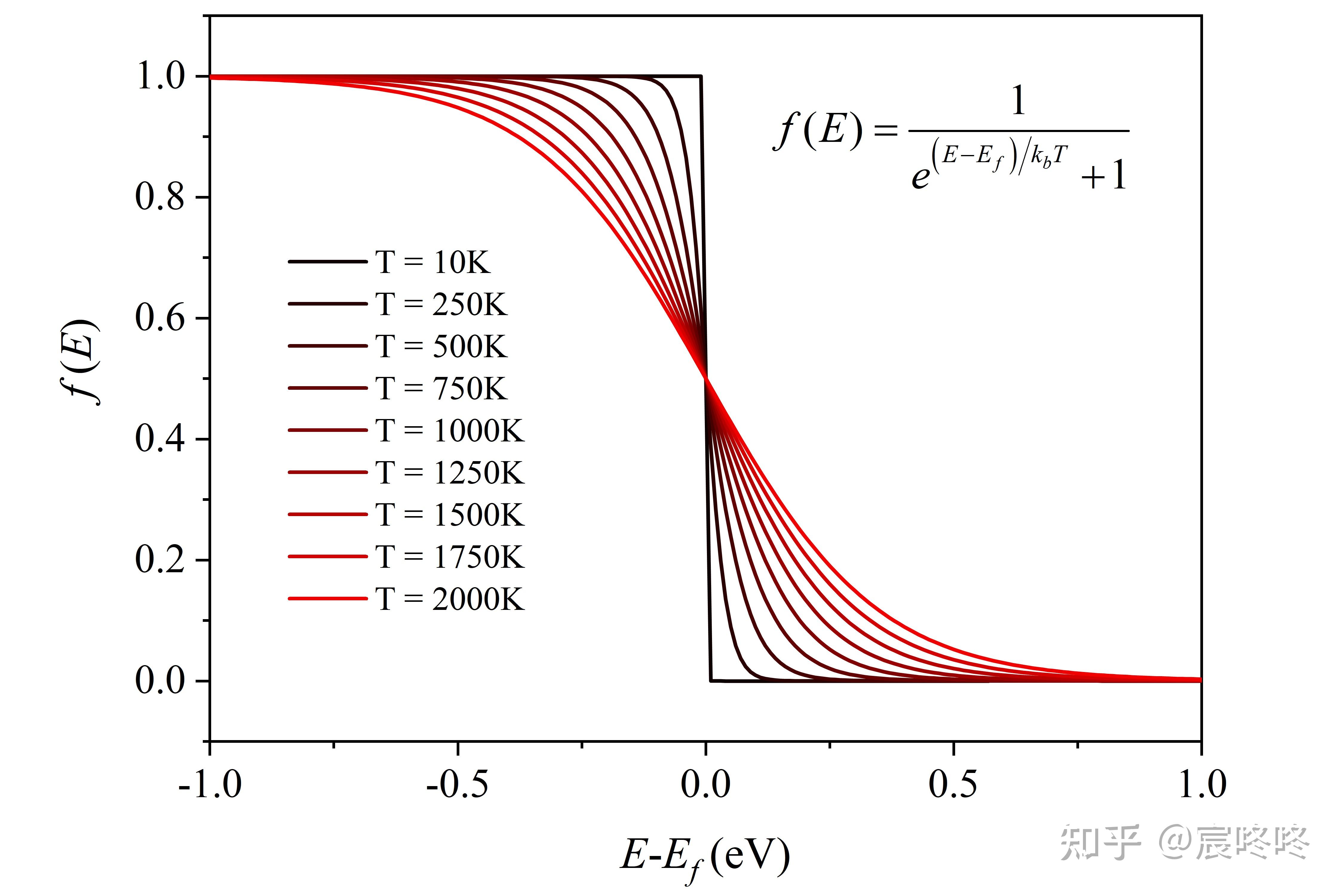 图片来源:知乎专栏
图片来源:知乎专栏
参考来源: [1] https://baike.baidu.com/item/费米-狄拉克统计/8644878 [2] https://zh.wikipedia.org/wiki/玻色–爱因斯坦统计