除了简谐振动,还有哪些其他类型的振动理论和模型?
参考资料

参考资料


Moonshot回答
除了简谐振动,还有多种振动理论和模型,包括但不限于:
-
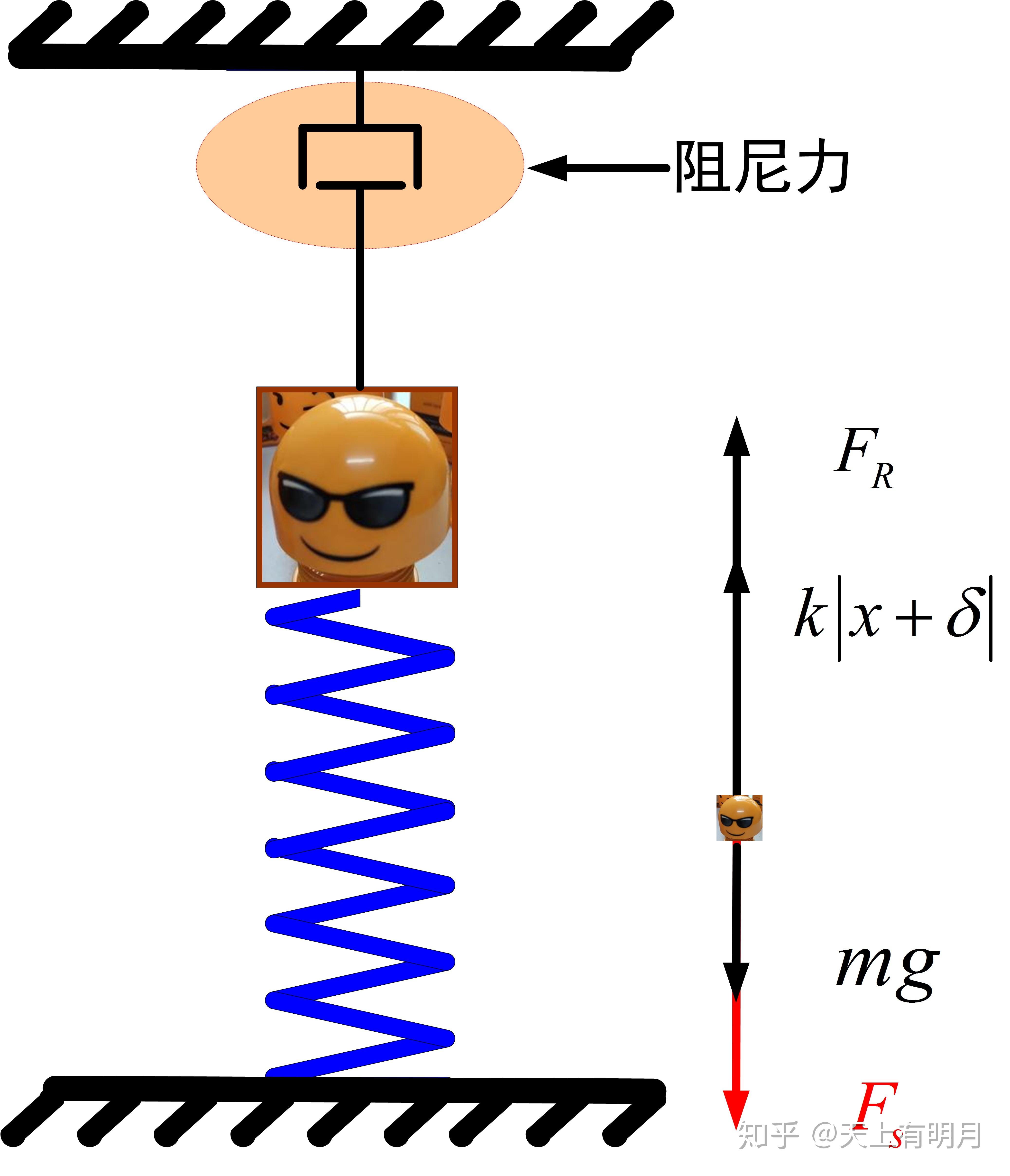
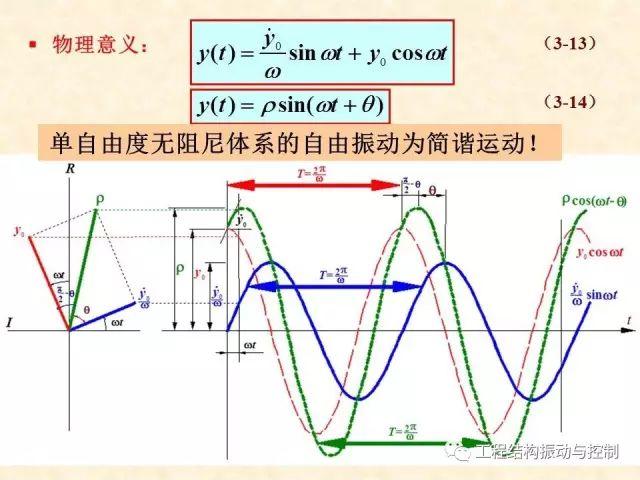
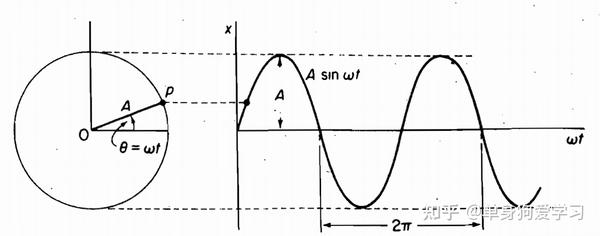
自由振动:系统在去掉外加干扰力之后出现的振动,这种振动靠弹性力、惯性力和阻尼力来维持。振动的频率就是系统的固有频率。
-
受迫振动:系统在外部周期性力作用下的振动。受迫振动的频率等于激励的频率,即使系统的固有频率发生变化。
-
阻尼振动:存在阻力(如摩擦力)时的振动。阻尼振动会因能量耗散而随时间衰减。
-
无阻尼振动:没有阻力影响的振动,理论上会无限持续下去。
-
单自由度系统振动:只在一个方向上振动的系统,如弹簧-质量模型。
-
多自由度系统振动:可以在多个方向上振动的系统,每个自由度对应一个固有频率。
-
连续体振动:如杆的纵向振动、梁的弯曲振动、板的振动等,这些模型考虑了材料的连续分布。
-
非线性振动:系统参数或外部激励是非线性时发生的振动,这类振动更为复杂,可能表现出混沌等复杂动态行为。
-
随机振动:由随机过程激励的振动,其响应也是随机的,适用于描述如地震、海浪等自然现象引起的振动。
-
复合振动:由多种振动类型组合而成的复杂振动。
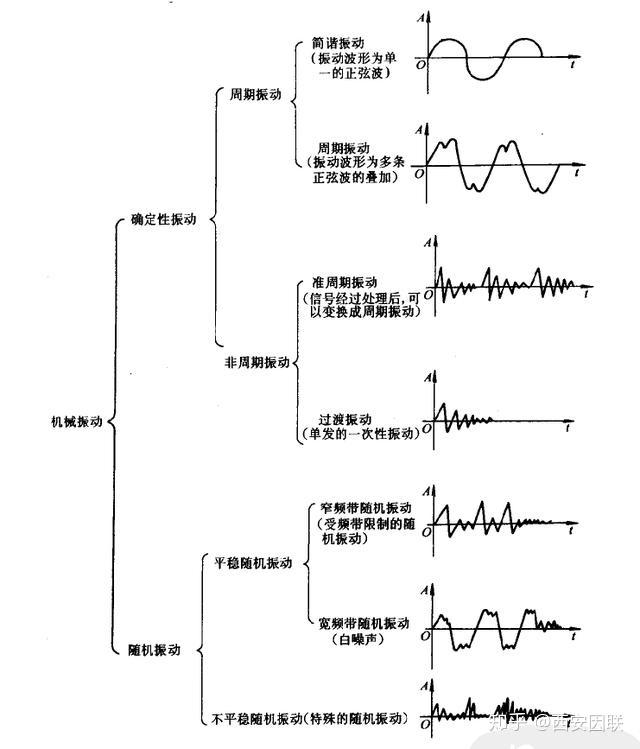
这些理论和模型有助于我们理解和分析各种工程和物理问题中的振动现象。例如,可以通过振动的分类和特点来了解机械设备的振动类型,包括周期振动、准周期振动、窄带随机振动和宽带随机振动等。此外,振动理论还涵盖了如杆的纵向振动、梁的弯曲振动等连续体振动问题,以及非线性振动和随机振动等更复杂的情况。这些理论和模型是振动分析和控制的基础,广泛应用于工程领域。