波函数的傅立叶变换在量子力学中有什么用途?
参考资料
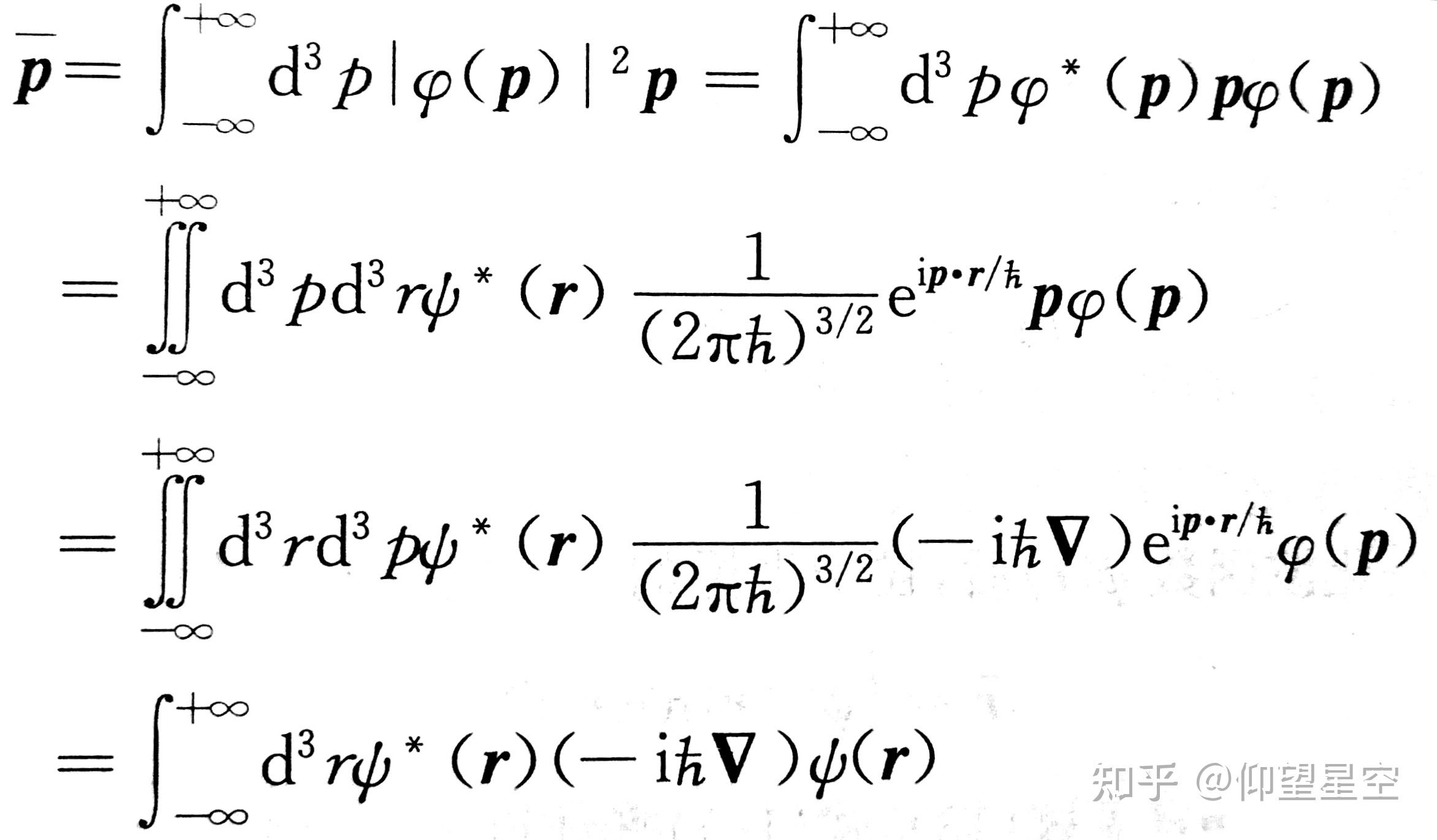
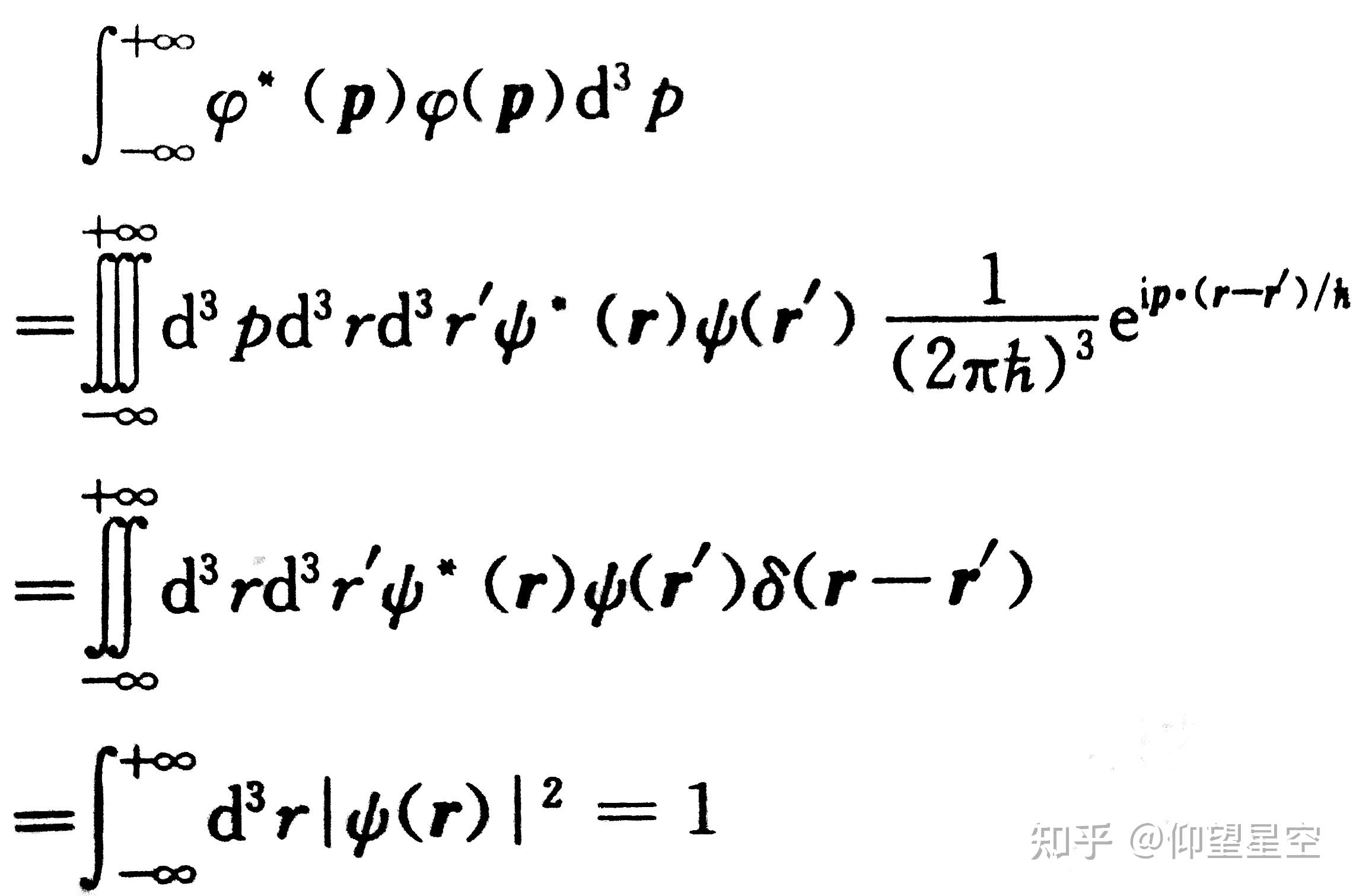
Moonshot回答
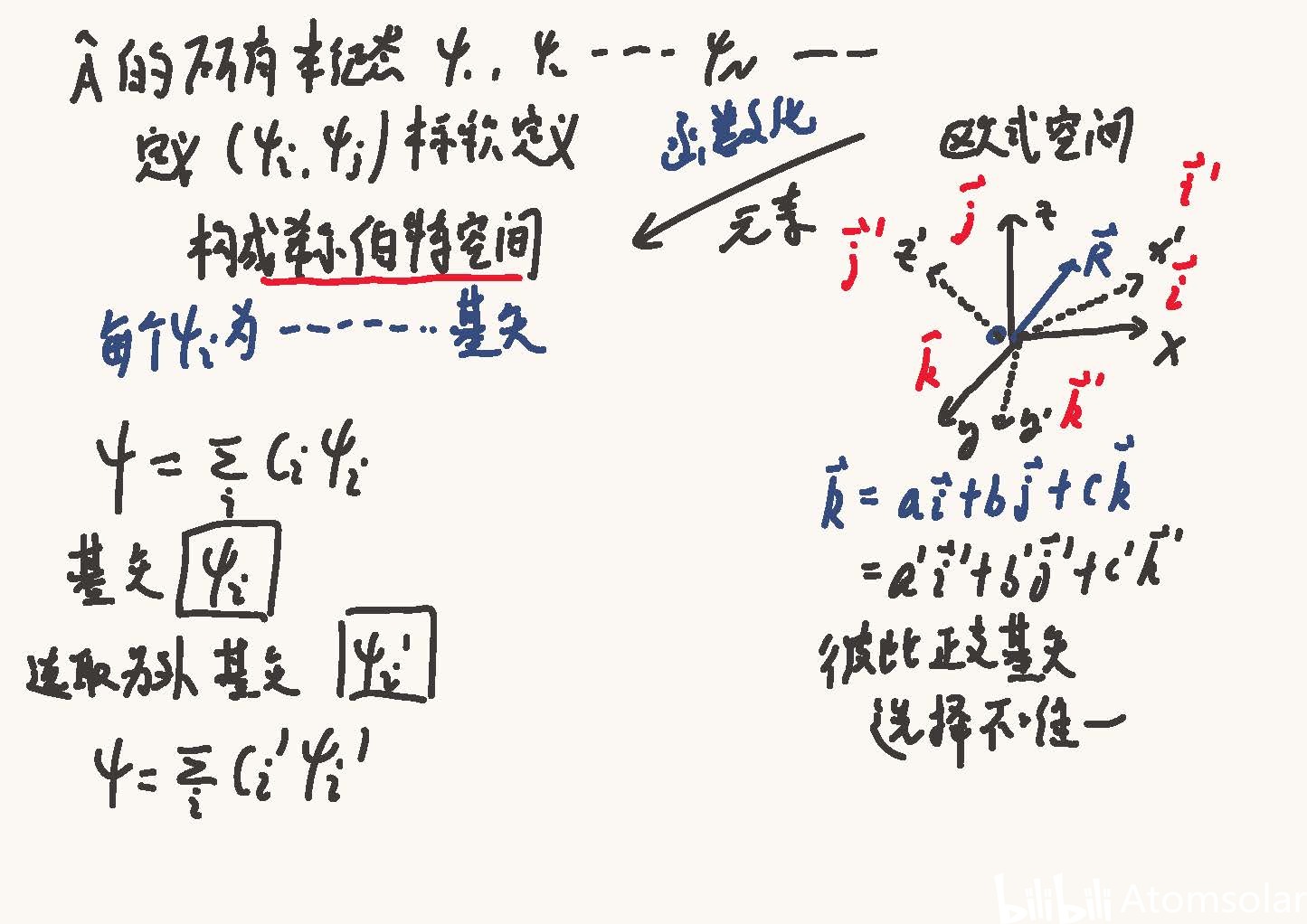
波函数的傅立叶变换在量子力学中具有重要的应用。它允许我们将波函数从位置空间(坐标空间)转换到动量空间,这在解决薛定谔方程和理解量子系统的性质时非常有用。傅立叶变换帮助我们确定粒子的动量分布,这是量子力学的一个基本方面。
此外,傅立叶变换在量子纠缠的检测、量子态的叠加和量子信息处理中也扮演着关键角色。例如,在量子计算中,量子傅立叶变换是Shor算法和量子相位估计等重要算法的组成部分。
从搜索结果中,我们可以看到傅立叶变换在量子力学中的应用非常广泛,包括但不限于:
- 波函数表示:波函数的傅立叶变换允许我们用动量本征态来表示波函数,从而分析系统在不同状态下的行为。
- 能量本征态表达:通过傅立叶变换,我们可以将能量算符转换为动量算符,进而求解能量本征值问题。
- 量子力学算符的变换:傅立叶变换可以应用于量子力学中的各种算符,以简化问题的求解过程。
此外,傅立叶变换在量子力学中的物理意义和重要性也得到了广泛讨论,它不仅是一个数学工具,更是理解和操作量子系统的基础。通过引用的搜索结果,我们可以进一步了解傅立叶变换在量子力学中的应用和重要性。