参考资料
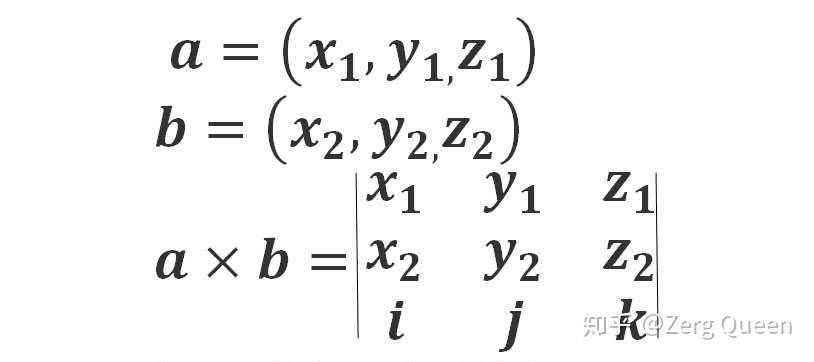



Moonshot回答
利用行列式计算两个向量的叉积是一种在三维空间中常用的方法。叉积的结果是一个垂直于原始两个向量的向量,其大小等于两个向量构成的平行四边形的面积,方向遵循右手定则。
计算两个向量 (\vec{a} = (a_1, a_2, a_3)) 和 (\vec{b} = (b_1, b_2, b_3)) 叉积的公式是:
[ \vec{a} \times \vec{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \end{vmatrix} ]
展开这个行列式,我们得到:
[ \vec{a} \times \vec{b} = (a_2b_3 - a_3b_2)\mathbf{i} - (a_1b_3 - a_3b_1)\mathbf{j} + (a_1b_2 - a_2b_1)\mathbf{k} ]
计算示例:
假设我们有两个向量 (\vec{a} = (1, 2, 3)) 和 (\vec{b} = (4, 5, 6)),我们想要计算它们的叉积。
根据上述公式,我们有:
[ \vec{a} \times \vec{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ 1 & 2 & 3 \ 4 & 5 & 6 \end{vmatrix} ]
展开这个行列式,我们得到:
[ \vec{a} \times \vec{b} = (2 \cdot 6 - 3 \cdot 5)\mathbf{i} - (1 \cdot 6 - 3 \cdot 4)\mathbf{j} + (1 \cdot 5 - 2 \cdot 4)\mathbf{k} ]
[ \vec{a} \times \vec{b} = (12 - 15)\mathbf{i} - (6 - 12)\mathbf{j} + (5 - 8)\mathbf{k} ]
[ \vec{a} \times \vec{b} = (-3)\mathbf{i} + (6)\mathbf{j} + (-3)\mathbf{k} ]
所以,叉积 (\vec{a} \times \vec{b} = (-3, 6, -3))。
这个计算过程可以通过行列式直观地完成,并且可以很容易地推广到更高维度的向量积计算中。在实际应用中,叉积在物理学中用于计算力矩和角动量,以及在计算机图形学中用于确定表面的法向量。
继续提问
相关问题
刘巴在刘备称帝前曾劝其暂缓称帝,这一建议背后有何深意?
在广东洪兵起义中,三合会的角色和影响力是怎样的?
西班牙语在历史上是如何受到巴斯克语影响的?
GOAT 作为全球最大的正品稀有球鞋交易平台,为什么选择中国作为其国际扩张的第一步?中国市场对它有何吸引力?
708年,唐朝在河套北岸修筑了三受降城,这一举措对当时的边疆防御有何重大意义?
现代化和数字化转型如何通过边缘技术提升客户互动和企业效率?
甌駱王国的建立者安阳王是如何通过“神机弩”来保卫国家的?
米特里达梯六世是如何通过毒药研究来保护自己的?
瓦尔代克和皮尔蒙特亲王国是如何从伯国升格为神圣罗马帝国亲王国的?
1327年议会对英格兰贵族与平民议员权力平衡有何重大影响?