如何进行贝特–萨尔皮特方程的数值求解?常用的数值方法有哪些?
参考资料

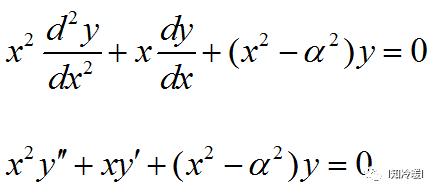

Moonshot回答
贝特-萨尔皮特方程(Bethe-Salpeter Equation,简称BSE)是量子场论框架下描述束缚态的相对论性方程。进行BSE的数值求解时,常用的数值方法包括:
- 变分法:通过最小化能量泛函来寻找基态和激发态的能量和波函数。
- 微扰法:将复杂的哈密顿量分解为简单的部分和微扰部分,然后逐步求解。
- 格林函数法:利用格林函数来求解非齐次方程,可以处理更复杂的相互作用。
- 有限元方法:将求解区域离散化,将连续问题转化为代数方程组求解。
- 平面波展开法:将波函数展开为平面波的叠加,适用于周期性边界条件的问题。
- 实空间网格法:在实空间中使用网格来离散化问题,适用于非周期性系统。
- GW近似:一种处理电子关联效应的方法,通过求解BSE来计算电子-空穴对的激发能。
这些方法各有优势和适用条件,选择合适的方法需要根据具体问题的性质和计算资源来决定。例如,变分法和微扰法适用于基态和低激发态的计算,而GW近似和BSE结合的方法则适用于更精确的电子结构计算。在实际应用中,可能需要结合多种方法来获得更准确的结果。