参考资料

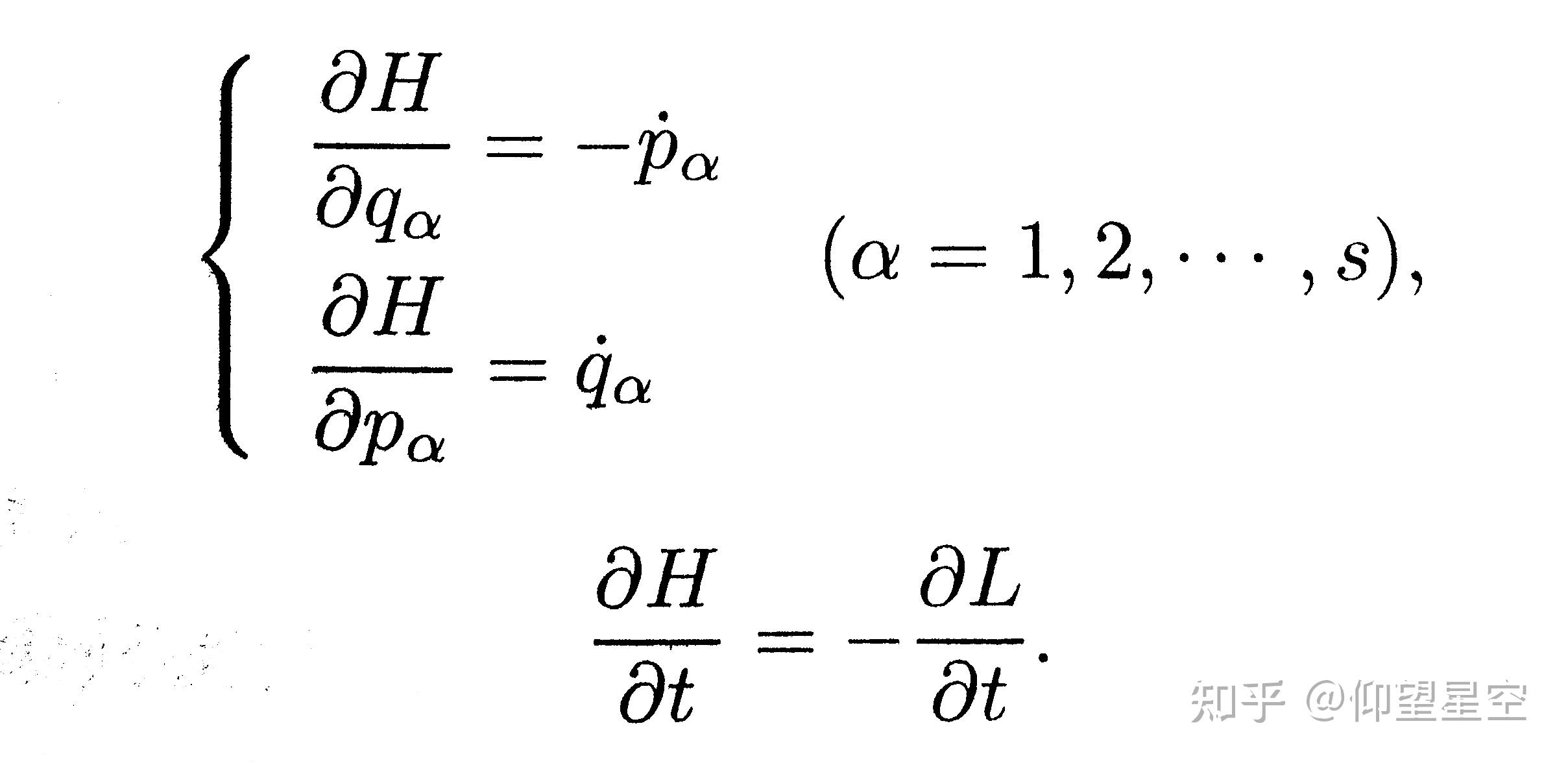


参考资料

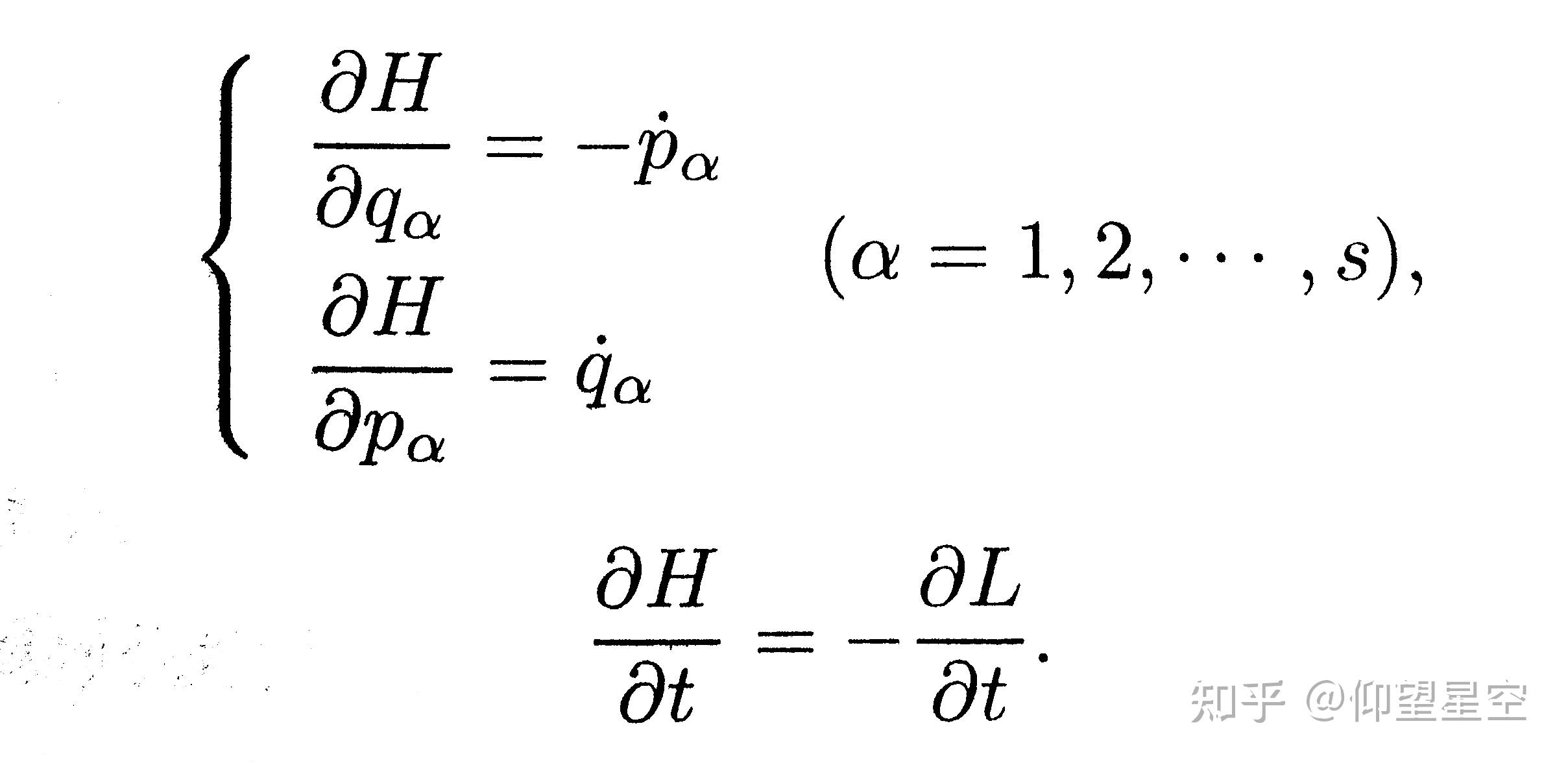

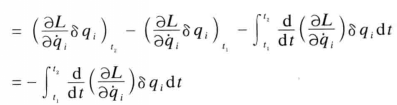
Moonshot回答
哈密顿-雅可比方程是经典力学中一个重要的偏微分方程,由哈密顿在19世纪初发现。它描述了系统的作用量随时间和位置的变化规律,是分析力学中一个基础方程。哈密顿-雅可比方程的一般形式为:
[ \frac{\partial S}{\partial t} + H\left(t, q, \frac{\partial S}{\partial q}\right) = 0 ]
其中,( S ) 是哈密顿主函数,( H ) 是哈密顿量,( t ) 是时间,( q ) 是广义坐标。
哈密顿-雅可比方程在解析动力学系统中的作用主要体现在以下几个方面:
-
简化问题:它将动力学问题转化为求解一个偏微分方程的问题,这在某些情况下可以简化问题的复杂性。
-
确定守恒量:哈密顿-雅可比方程在辨明守恒的物理量方面特别有用,即使物理问题本身无法完全解析,该方程仍能正确辨明守恒量。
-
最小作用量原理:哈密顿-雅可比方程可以推导出最小作用量原理与费马原理,是分析力学和几何光学之间的桥梁。
-
可积系统:在可积系统中,哈密顿-雅可比方程可以用来寻找系统的精确解。
-
量子力学基础:在量子力学的发展中,哈密顿-雅可比方程为波函数的引入提供了理论基础。
-
控制理论:在最优控制理论中,哈密顿-雅可比-贝尔曼方程是求解最优控制问题的关键。
哈密顿-雅可比方程不仅在理论物理学中占有重要地位,还在光学、量子力学、控制理论等领域有着广泛的应用。通过求解哈密顿-雅可比方程,可以更深入地理解物理系统的行为和演化规律。
继续提问
相关问题
如何通过哈密顿-雅可比方程得到作用量函数S的解?
哈密顿-雅可比方程的主要应用是什么?
什么是作用量-角度坐标,它在经典力学中有哪些应用?
为什么虽然理论中宣称没有太大的物理意义,但物理学家仍然会将四维时空切割为三维空间剖面?
《天才王子的赤字国家重生术》的片尾曲《ヒトリとキミと》的作词者和作曲者分别是谁?
土星奖最佳动画电影奖项在早期的1978年和1982年分别颁发了哪些电影?
如何在传统四年制学位之外选择适合自己的混合或非标准学术体验?
什么是15世纪英格兰音乐风格“Contenance Angloise”的独特之处?
《西鹤一代女》改变自哪位日本作家的作品,该作家还有哪些知名的作品?
现代化理论如何为中国等国家的快速发展提供指导?