什么是拓扑弦论,它在弦论中的作用和意义是什么?
参考资料

参考资料

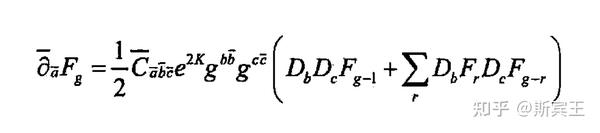

Moonshot回答
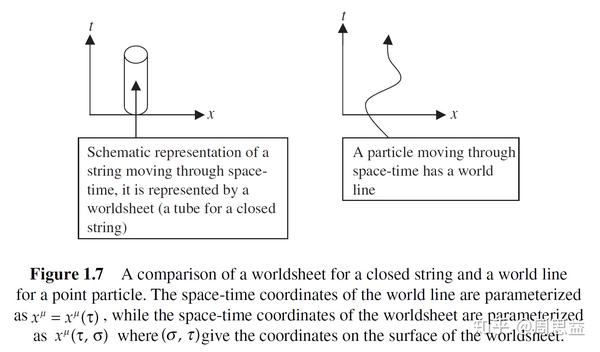
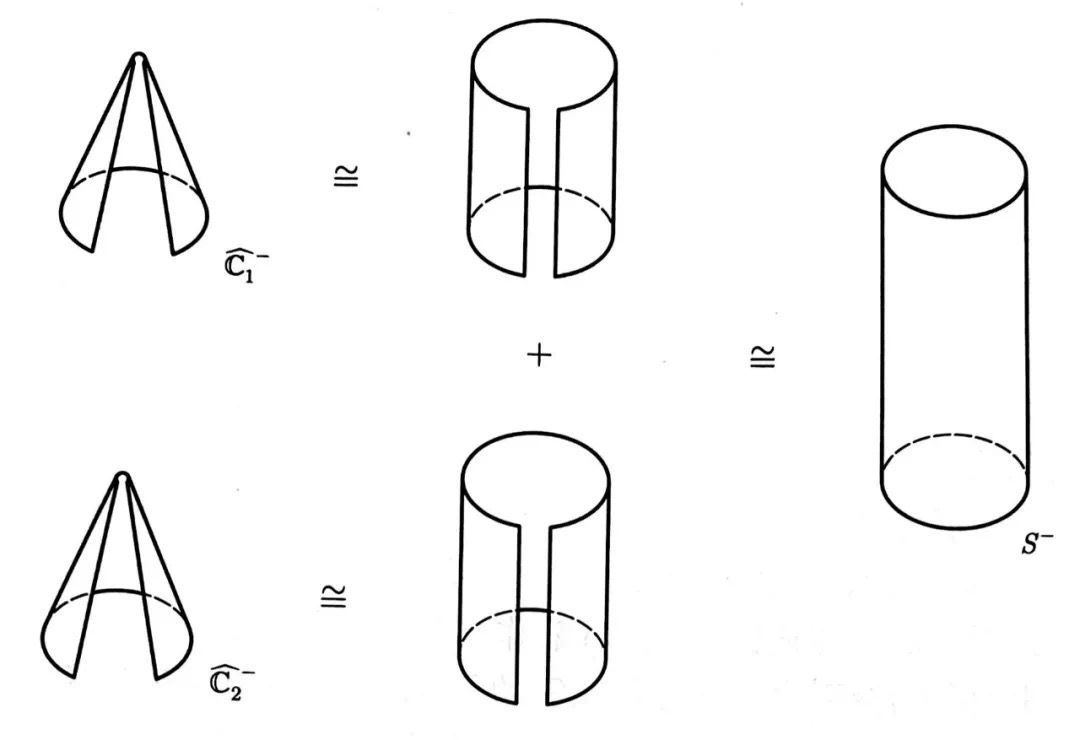
拓扑弦论是一种理论物理中的弦论形式,它专注于研究那些在特定的时空背景下,其物理性质仅依赖于拓扑结构而不依赖于时空的具体几何形状的弦理论。这种理论由爱德华·威滕于1988年提出,通过拓扑扭曲来修改sigma模型,从而使得理论具有拓扑性。拓扑弦论有两个U(1)对称,即R-对称,洛伦兹对称也要通过结合转动与R-对称来修改。我们可以用两种R-对称中的任一种,产生两种不同的理论,即A模型与B模型。
拓扑弦论在弦论中的作用和意义非常重要。它不仅为理解弦论提供了新的视角,还对数学和物理学的其他领域产生了深远的影响。例如,拓扑弦论在三维经典统计领域取得了显著进展,发展了一套数学上的拓扑不变量的计算方法。它与二维量子可积系统有深刻的联系,可能对低维物理的拓扑计算带来革命性的进展。此外,拓扑弦论还与弦拓扑有紧密的联系,后者在辛几何、纽结理论、同伦论以及数学物理中都有重要的应用。
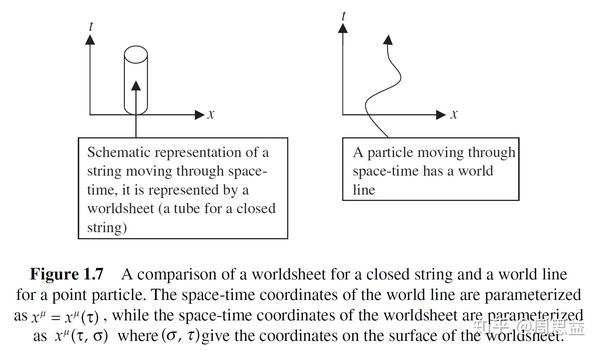
总的来说,拓扑弦论是弦论中一个非常活跃且具有重要意义的分支,它不仅推动了弦论本身的发展,还促进了数学和物理学其他领域的交叉融合。更多关于拓扑弦论的信息,可以参考维基百科和百度百科上的详细解释。