什么是希尔伯特空间,它在量子力学中的作用是什么?
参考资料


参考资料


Moonshot回答
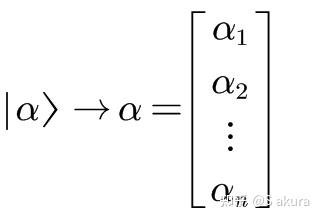
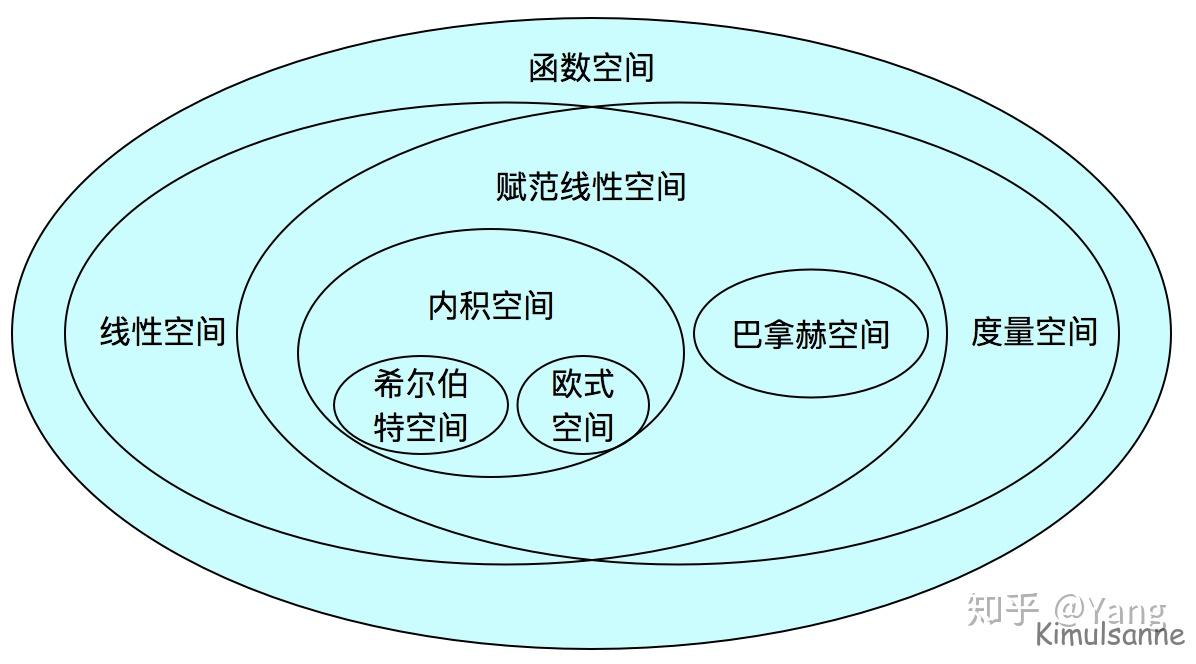
希尔伯特空间是数学中的一个概念,它是一个完备的内积空间,这意味着它是一个带有内积的完备向量空间。内积的构造推广了欧几里得空间的距离和角的概念,而完备性确保了空间内所有的柯西序列都收敛到空间内的某一点。这使得许多微积分中的概念都可以在希尔伯特空间中使用。
在量子力学中,希尔伯特空间扮演着至关重要的角色。量子力学本质上是希尔伯特空间及作用在其上的算子的理论。量子态可以被表示为希尔伯特空间中的向量,称为态矢。量子系统的可观测量,如位置和动量,对应于希尔伯特空间中的厄米算子。量子态的时间演化遵循薛定谔方程,也可以在希尔伯特空间的框架内描述。
此外,量子力学中的波函数本质上是希尔伯特空间中的函数,其中两个函数的内积以积分形式表示。这允许我们计算量子态的概率幅和概率,这是量子力学预测实验结果的基础。

总的来说,希尔伯特空间为量子力学提供了一个严谨的数学框架,使得我们可以精确地描述和预测量子系统的行为。更多关于希尔伯特空间在量子力学中作用的详细信息,可以参考知乎上的量子力学入门-希尔伯特空间专栏文章。