为什么向量叉积结果会受到右手定则的影响?
参考资料

Moonshot回答
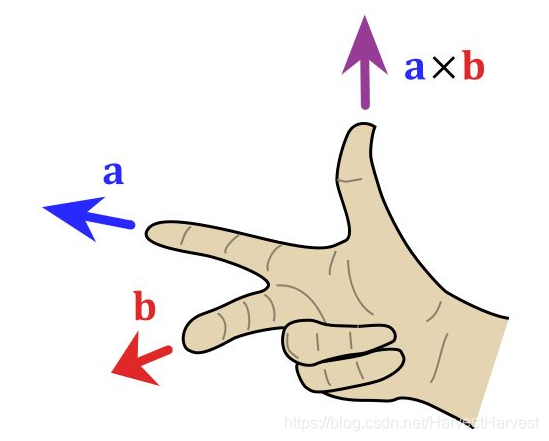
向量叉积的结果受到右手定则的影响,是因为右手定则提供了一种确定叉积方向的直观方法。根据右手定则,如果你将右手的食指指向第一个向量的方向,中指指向第二个向量的方向,并且这两个向量都在旋转进入彼此的平面,那么你的拇指将指向叉积向量的方向。这个规则帮助我们理解叉积不仅具有大小,而且具有方向,它垂直于参与叉积的两个原始向量所定义的平面。
叉积的大小由两个向量的大小和它们之间夹角的正弦值的乘积决定,而方向则由右手定则确定。这种方向的确定对于理解物理现象如力矩和角动量非常重要,因为这些物理量都是向量,并且它们的计算涉及到叉积。
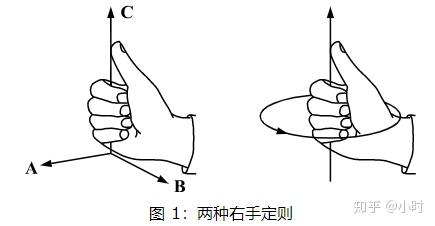
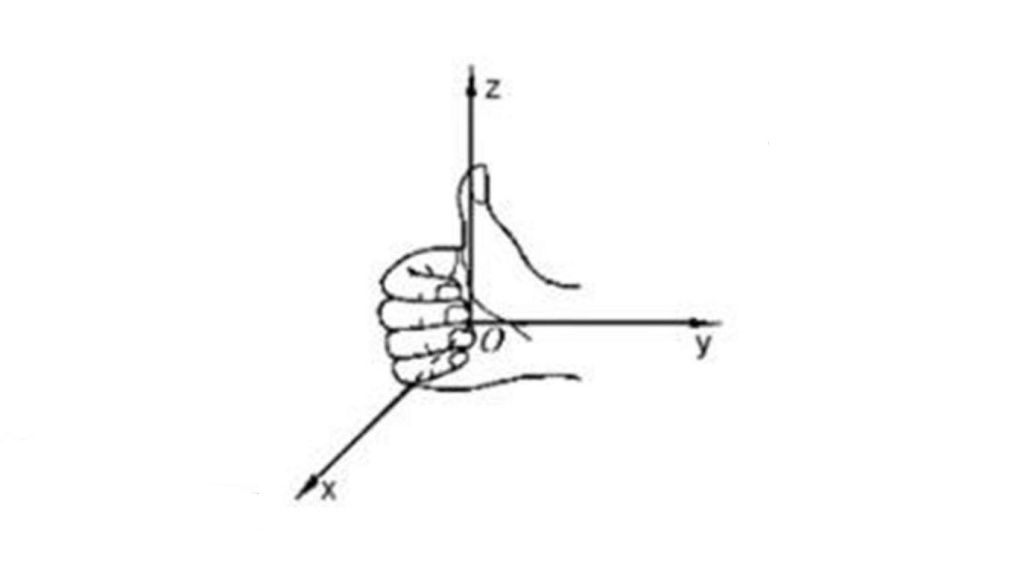
以下是一些与向量叉积和右手定则相关的图像,可以帮助直观理解这一概念:
这些图像展示了如何使用右手定则来确定两个向量的叉积的方向,这是理解和计算叉积的一个重要方面。更多详细信息可以参考相关文章,如矢量积(叉积)与"右手定则"。