什么是哈密顿动力学中的运动常数,它如何影响系统动态?
参考资料
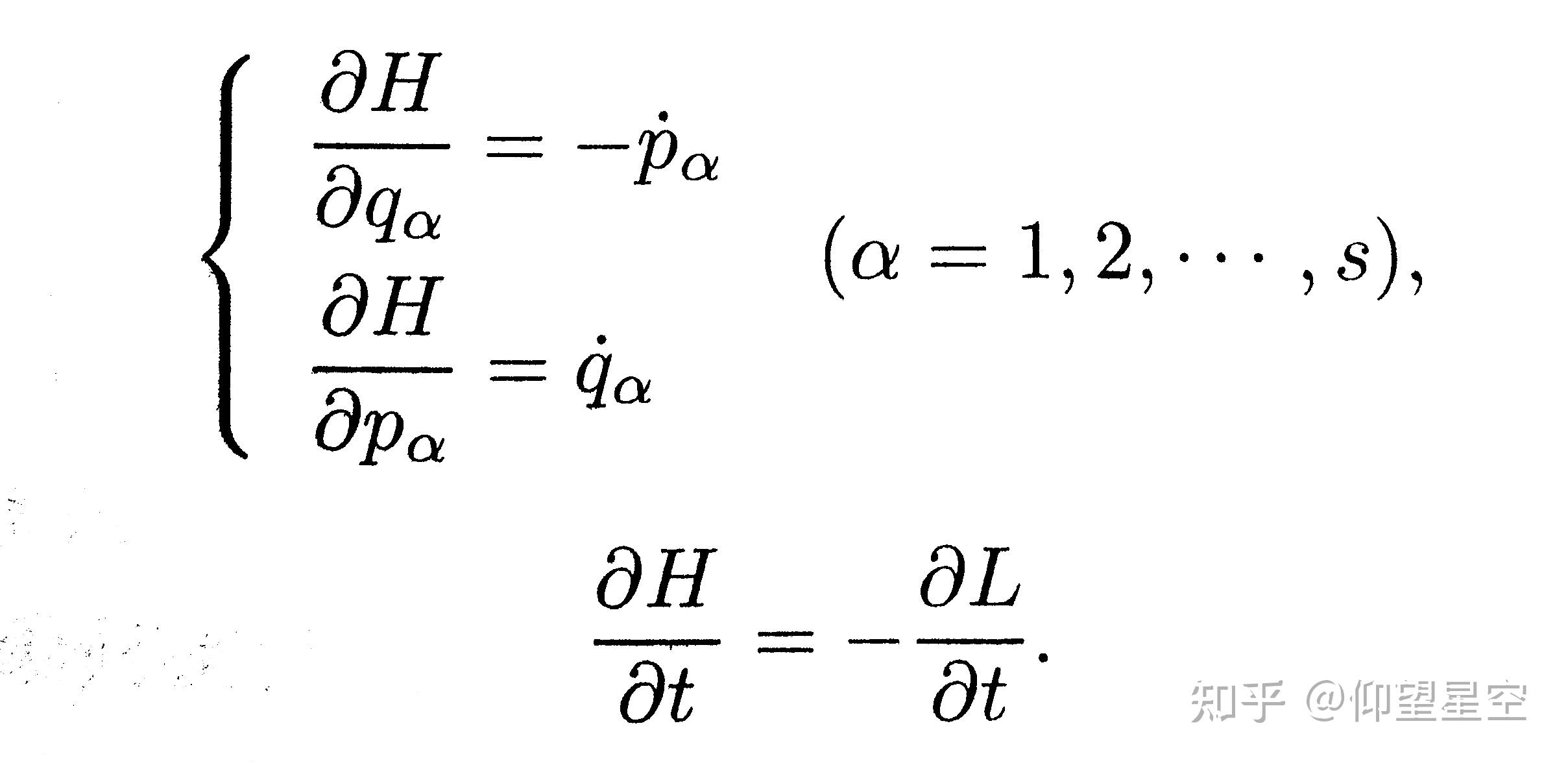


Moonshot回答
在哈密顿动力学中,运动常数指的是那些在系统随时间演进过程中保持不变的物理量,也称为守恒量。这些常数类似于运动的约束,但它们是数学上的约束,自然地从运动方程式中显现出来,而不是物理的约束。运动常数的存在对系统动态有重要影响,因为它们提供了对系统演化的额外约束,从而减少了系统的自由度。
例如,能量、动量和角动量是常见的运动常数。在哈密顿力学中,哈密顿函数(H)是一个重要的运动常数,它代表系统的总能量。如果哈密顿量不显式地依赖于时间,那么能量就是守恒的。这意味着系统随时间演化,其总能量保持不变。
此外,根据哈密顿正则方程,哈密顿函数的导数如果为零,表明相应的物理量是守恒的。这些守恒定律可以大大简化复杂系统的动力学分析,因为它们允许我们忽略某些自由度,从而减少需要解决的方程数量。
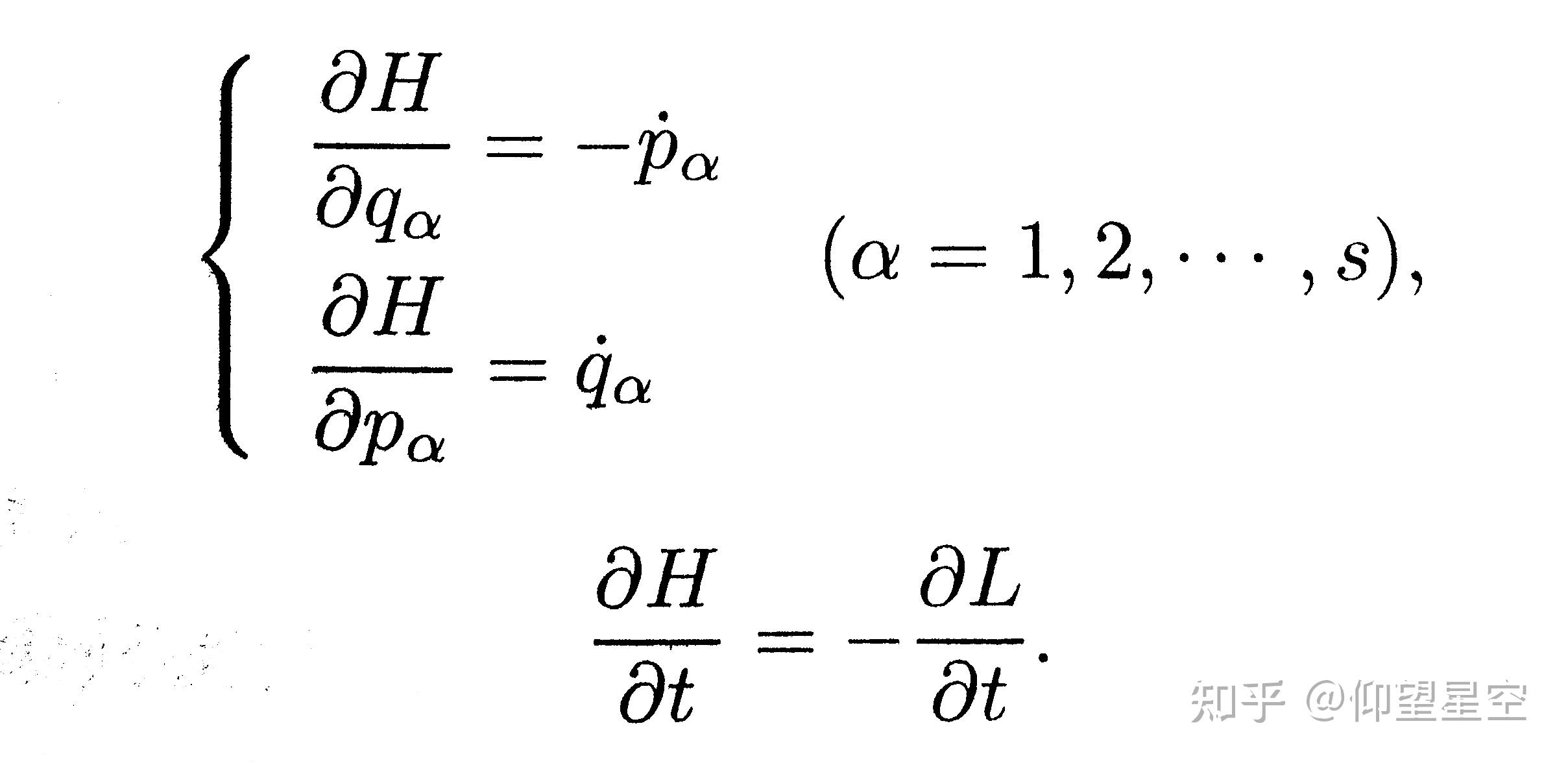 图片来源:知乎专栏
图片来源:知乎专栏
运动常数在哈密顿动力学中的作用是多方面的,它们不仅帮助我们理解系统的演化规律,还可以用于预测系统的未来行为。例如,如果我们知道系统的初始状态和所有运动常数,我们就可以预测系统在任何未来时间的状态。这些常数是哈密顿动力学中不可或缺的组成部分,对于理解和分析物理系统具有重要意义。更多信息可以参考维基百科。