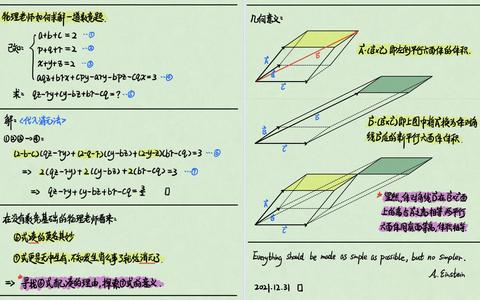
如何用标量三重积来计算平行六面体的体积?
参考资料

Moonshot回答
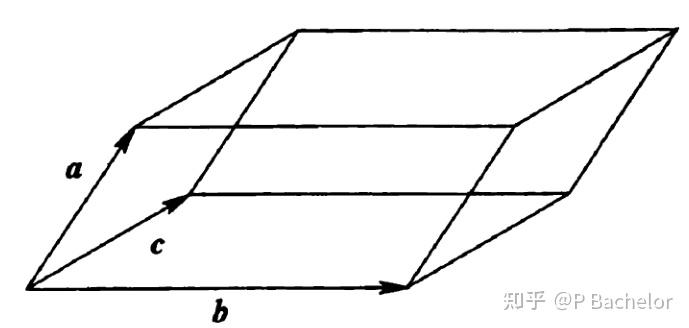
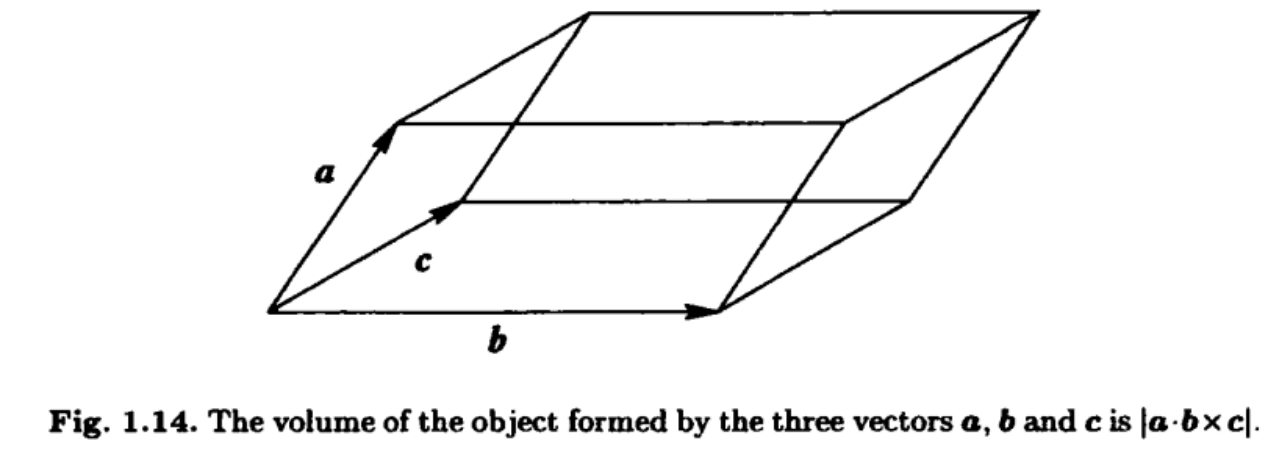
平行六面体的体积可以通过标量三重积来计算。标量三重积是三个向量的运算,结果是一个标量值,其计算公式为 (\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C}))。在几何上,标量三重积的绝对值表示由三个向量构成的平行六面体的体积。具体来说,如果三个向量 (\mathbf{a})、(\mathbf{b}) 和 (\mathbf{c}) 构成一个平行六面体,那么这个平行六面体的体积 (V) 可以通过下面的公式计算:
[ V = |\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})| ]
标量三重积的计算在向量微积分、几何学以及确定由三个向量构成的平行六面体的体积中非常有用。它不仅用于数学领域,还在物理和工程领域有应用,例如计算扭矩和角动量。
以下是一些有用的资源,可以帮助你进一步了解标量三重积和平行六面体体积的计算:
此外,还有几个图像资源可以帮助可视化这一概念:


