参考资料

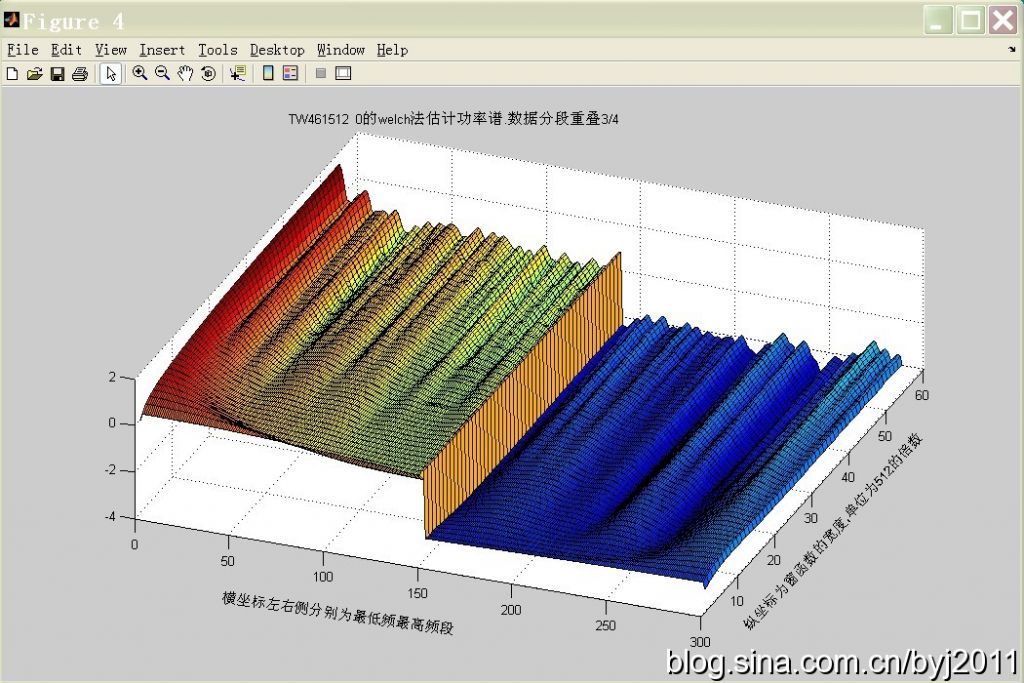
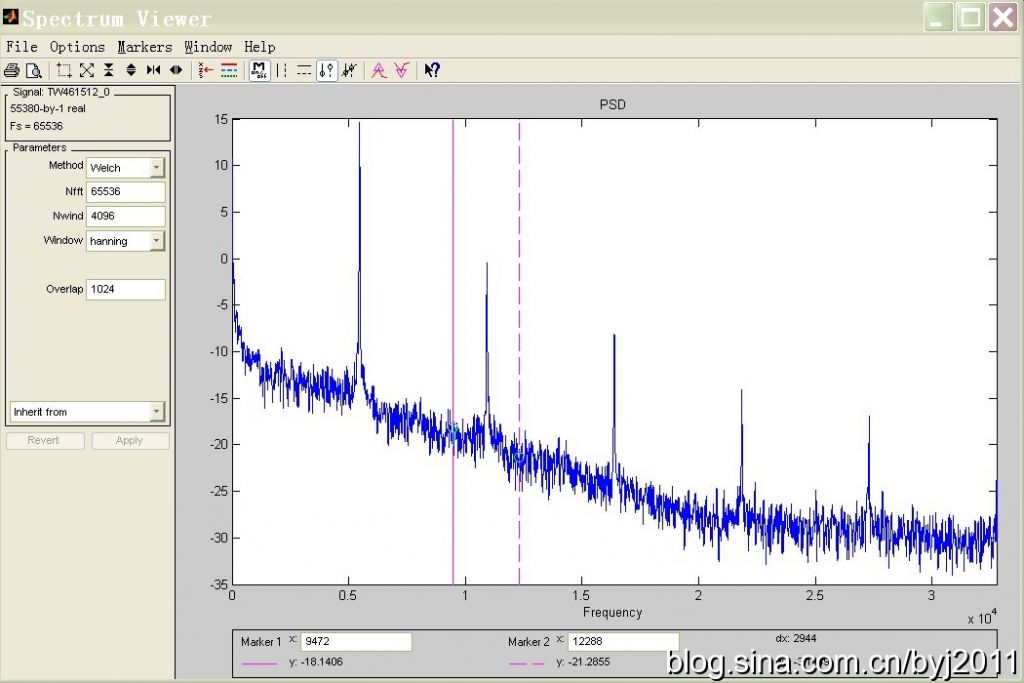
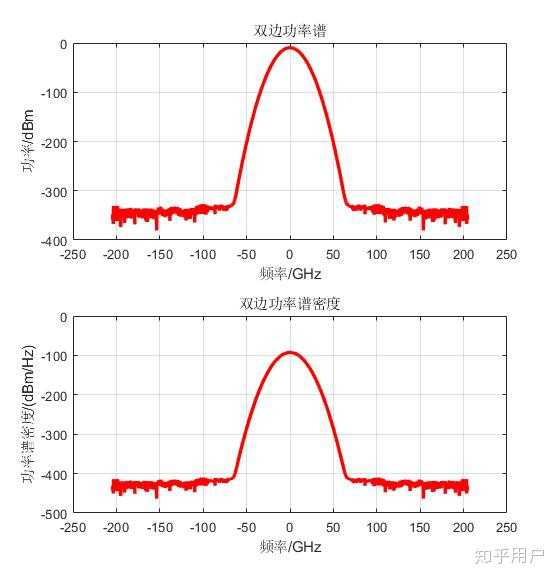
使用Welch法估计信号的功率谱密度（PSD）是一种常用的方法，它通过将信号分成重叠的段，对每段数据加窗，然后计算每段的周期图，最后对所有周期图求平均来得到功率谱密度的估计。以下是使用Welch法估计信号功率谱密度的基本步骤：

1. 准备数据：首先，你需要有一个时间序列数据集，它是你想要分析的信号。

2. 选择窗函数：Welch法需要一个窗函数来减少频谱泄漏。常用的窗函数包括汉明窗（Hamming）、汉宁窗（Hanning）和布莱克曼窗（Blackman）等。

3. 分段和重叠：将信号分成多个段，每段可以有重叠部分。这样做可以提高频率分辨率并减少边缘效应。

4. 计算每段的周期图：对每一段数据应用窗函数，然后计算每段的快速傅里叶变换（FFT），得到每段的周期图。

5. 平均周期图：将所有段的周期图平均，得到功率谱密度的估计。

在MATLAB中，可以使用pwelch函数来实现Welch法。而在Python中，可以使用SciPy库中的welch函数。这些函数通常需要输入信号、采样频率、窗函数、段的重叠比例等参数。

例如，在MATLAB中，你可以使用以下代码来估计信号的功率谱密度：

% 假设x是你的信号，Fs是采样频率
window = hamming(length(x)); % 选择窗函数
noverlap = 100; % 定义重叠样本数
nfft = 1024; % FFT点数
[pxx, f] = pwelch(x, window, noverlap, nfft, Fs);

在Python中，使用SciPy的示例代码如下：

from scipy.signal import welch
import numpy as np
import matplotlib.pyplot as plt

# 假设x是你的信号，fs是采样频率
fs = 1000  # 采样频率1000Hz
frequencies, power = welch(x, fs, window='hamming', nperseg=100, noverlap=50, scaling='density')

plt.semilogy(frequencies, power)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Power/Frequency [dB/Hz]')
plt.show()

通过这些步骤和代码示例，你可以使用Welch法来估计信号的功率谱密度。搜索结果中还提供了一些有用的资源和图像，可以帮助你更深入地理解Welch法及其应用。