参考资料

几何代数提供了一种强大的数学工具，用于简化计算机图形学中的三维旋转。通过使用几何代数，可以更简洁地表示和计算三维空间中的旋转，从而提高计算效率和精度。

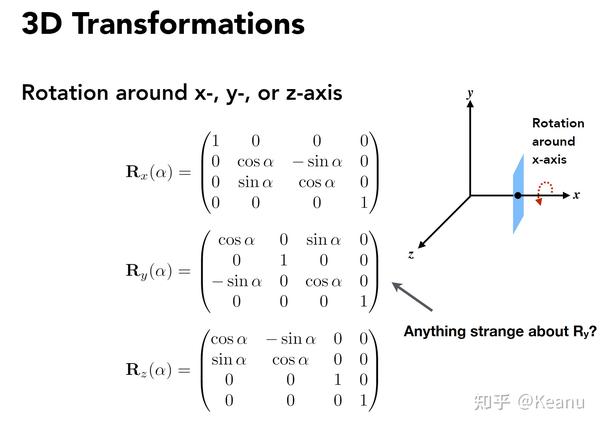
三维旋转在计算机图形学中通常涉及旋转矩阵、欧拉角和四元数等概念。旋转矩阵虽然直观，但在处理过程中容易受到万向节死锁的影响。欧拉角表示直观，但同样存在万向节死锁问题，且在插值时难以避免奇异性。四元数则提供了一种无奇异性且计算效率高的解决方案，但需要较高的数学基础才能理解。

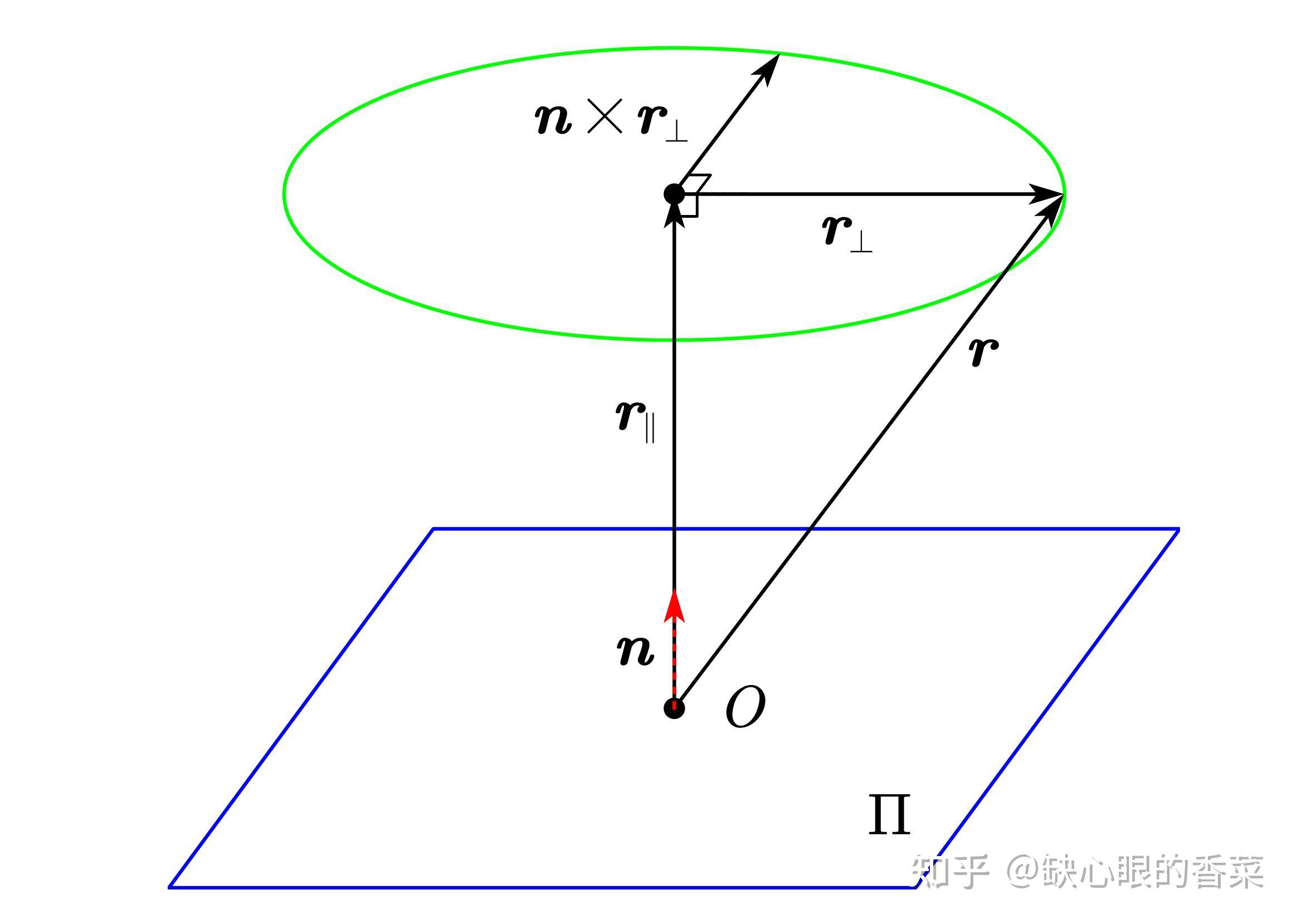
几何代数通过多维几何对象（如向量、双矢量和伪矢量）提供了一种统一的数学框架来表示和操作三维空间中的旋转。这种方法可以避免传统方法中的一些限制，例如万向节死锁和插值问题。几何代数中的一些关键概念，如反演、对偶数和几何积，为三维旋转提供了新的视角和计算方法。

此外，几何代数还提供了一种直观的方式来表示和计算旋转的合成和分解，这对于计算机图形学中的动画和仿真尤为重要。通过几何代数，可以更容易地实现旋转的插值和逼近，从而生成平滑且逼真的动画效果。

总的来说，几何代数为计算机图形学中的三维旋转提供了一种简洁、高效且强大的数学工具，有助于提高图形处理的性能和质量。通过进一步的研究和应用，几何代数有望在计算机图形学领域发挥更大的作用。