参考资料

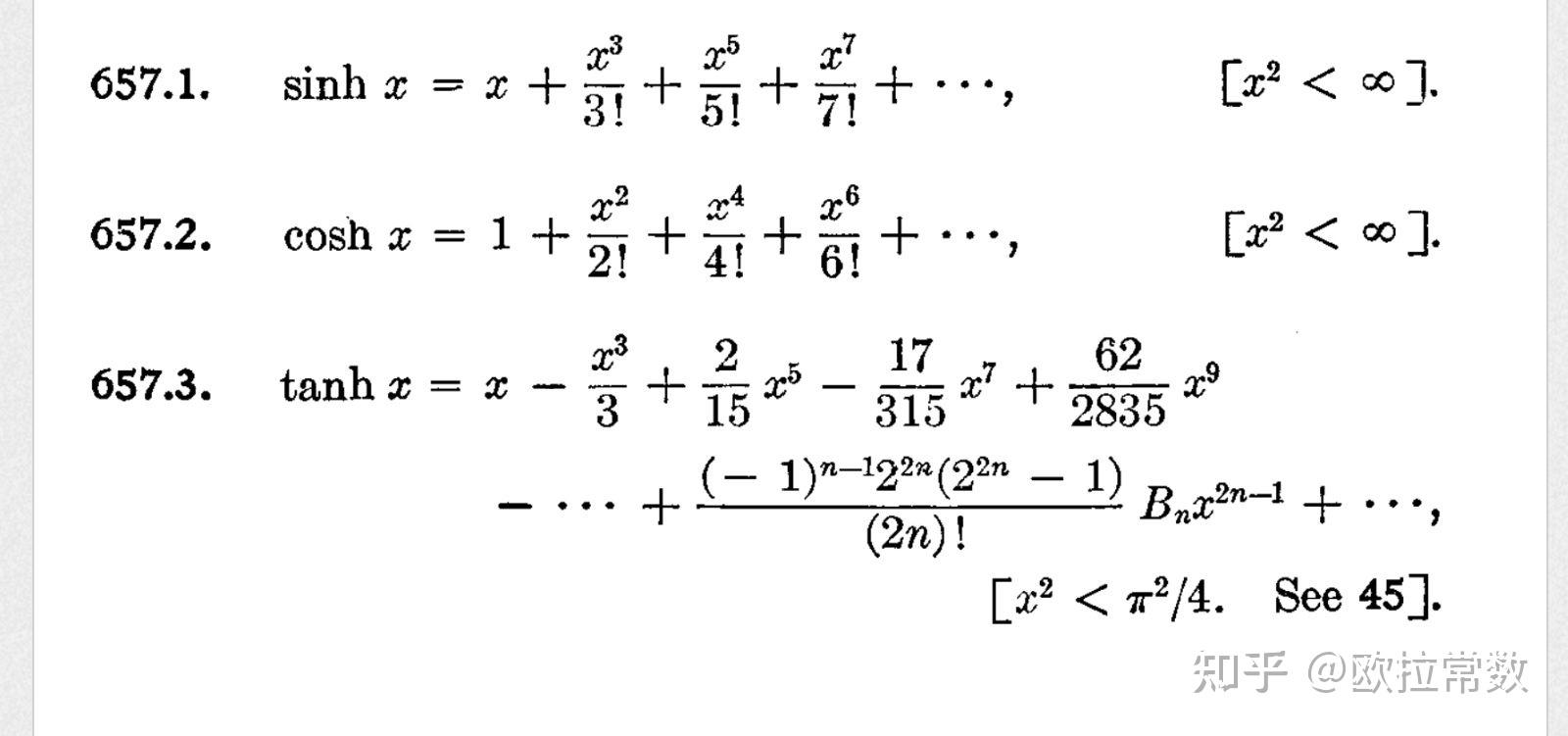
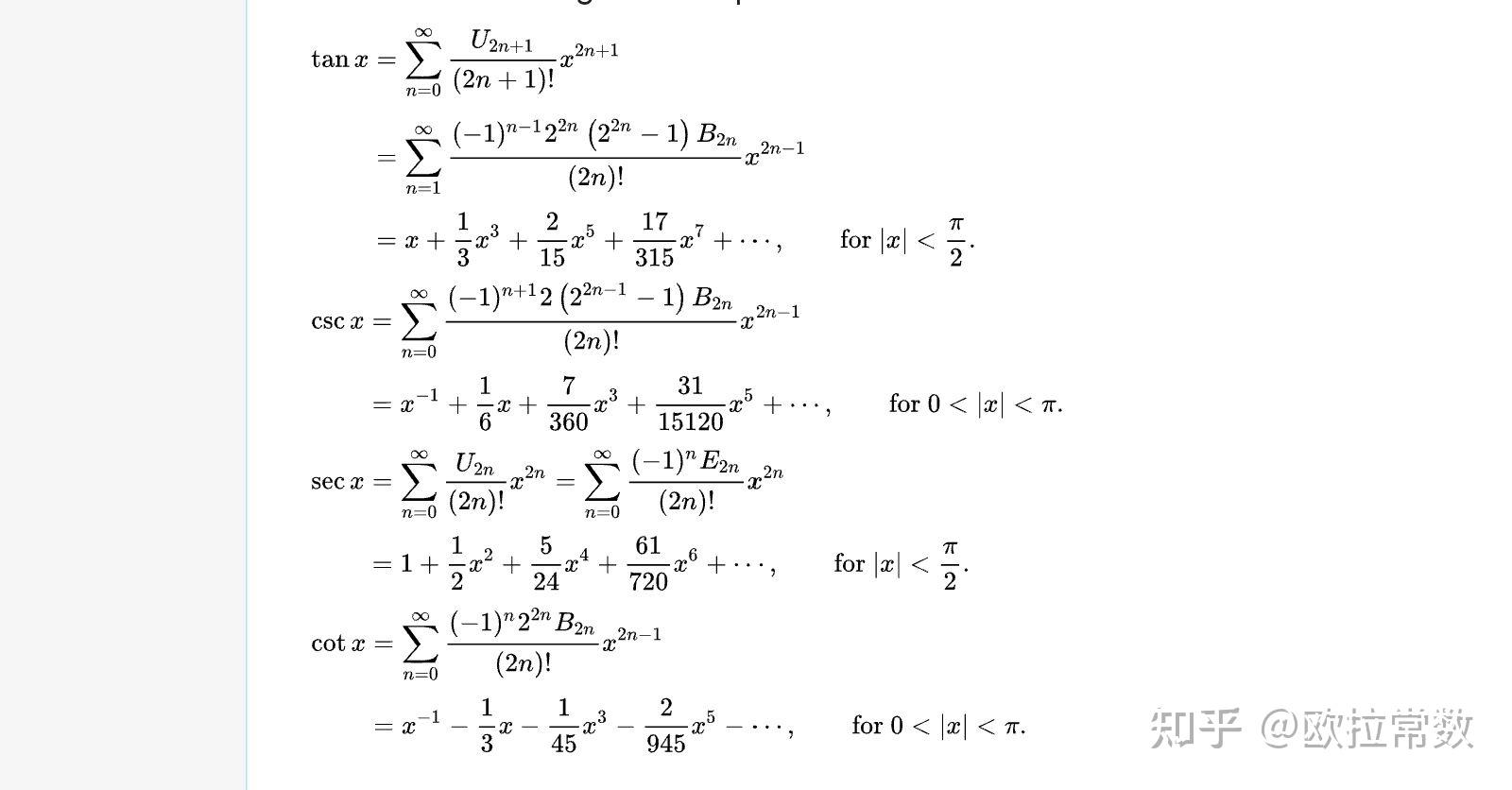

参考资料



Moonshot回答
通过泰勒级数展开证明低速度下的动能表达式与经典力学的一致性,我们可以从相对论动能公式出发。相对论动能公式为 (E_k = (\gamma - 1)mc^2),其中 (\gamma) 是洛伦兹因子,定义为 (\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}})。在低速度((v \ll c))情况下,我们可以将洛伦兹因子 (\gamma) 通过泰勒级数展开来近似。
泰勒级数展开的一般形式为: [ f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots ]
将 (\gamma) 在 (v=0) 处进行泰勒展开,我们得到: [ \gamma = 1 + \frac{1}{2}\frac{v^2}{c^2} + \frac{1}{8}\frac{v^4}{c^4} + \cdots ]
将这个展开式代入相对论动能公式,我们得到: [ E_k = \left(1 + \frac{1}{2}\frac{v^2}{c^2} + \frac{1}{8}\frac{v^4}{c^4} + \cdots - 1\right)mc^2 ] [ E_k = \left(\frac{1}{2}\frac{v^2}{c^2} + \frac{1}{8}\frac{v^4}{c^4} + \cdots\right)mc^2 ]
在低速度极限下,高阶项(如 (v^4) 项)可以忽略,因此我们得到: [ E_k \approx \frac{1}{2}mv^2 ]
这正是经典力学中的动能表达式。因此,通过泰勒级数展开,我们证明了在低速度极限下,相对论动能表达式与经典力学的动能表达式是一致的。这一证明过程展示了物理理论在不同速度极限下的平滑过渡和统一性。来源
继续提问
相关问题
哪位导演在第47届威尼斯影展上获得了最佳导演奖?
德川家康在关原之战后如何巩固自己的权力?
在生活中有哪一些实例可以用来解释加速度的概念?
米列夫岩为何以保加利亚诗人命名,他有什么特别的贡献吗?
1931年4月1日,何应钦奉蒋介石命率部队20余万人对江西中央苏区红军进行第二次“围剿”,采用了什么作战方针?
吴君如在1990年代有哪些音乐成就,她曾获得过哪些音乐奖项?
傅科摆与冷泽-提尔顿进动之间的关系是什么?
乔赛亚·罗伊斯在哈佛大学执教30余年,他的哪些思想对后来的哲学家产生了深远影响?
《源氏物语》为何被誉为世界上最早的长篇写实小说?
电影《花吃了那女孩》的配乐是由哪位音乐人创作的,包含了哪些主题曲?