连续映射定理中的度量空间是指什么,它在这一定理中的作用和具体含义是怎样的?
参考资料




参考资料



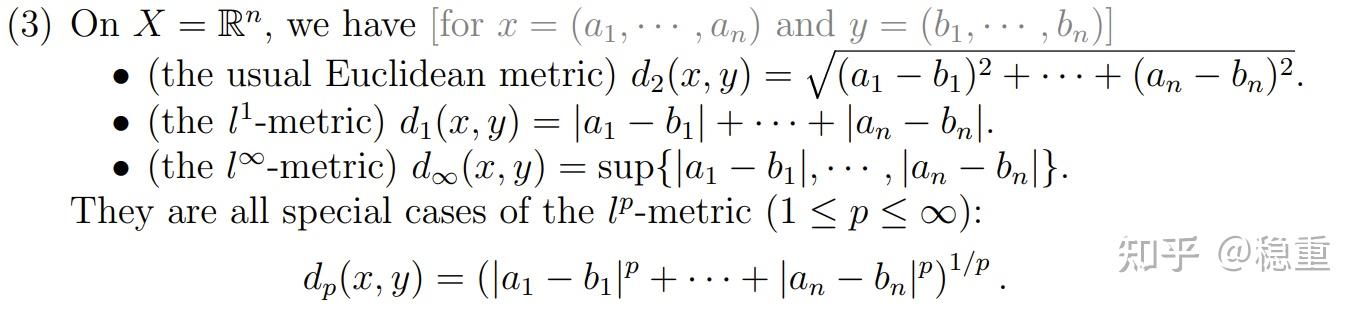
Moonshot回答
度量空间是数学中的一个基本概念,它由一个集合和一个定义在该集合上的距离函数组成,这个距离函数满足非负性、同一性、对称性和三角不等式。在连续映射定理中,度量空间的作用是提供一个框架来讨论映射的连续性。连续映射定理表明,如果一个函数在度量空间中是连续的,那么它将收敛的点列映射为收敛的像点列。
在度量空间中,连续性可以通过“(\delta-\varepsilon)”语言来定义,即对于任意给定的正数(\varepsilon),存在一个正数(\delta),使得当点列在度量空间中的原像距离小于(\delta)时,其像点列的距离也小于(\varepsilon)。此外,度量空间中的连续映射不一定保持度量,但可以定义更强的映射要求,如等距嵌入,它要求映射保持所有点对之间的距离。
度量空间的紧致性是连续映射定理中的一个重要概念,紧致度量空间具有完备性和完全有界性。这意味着在紧致度量空间中,每个Cauchy序列都有收敛的子序列,从而保证了映射的连续性。
总的来说,度量空间在连续映射定理中的作用是提供了一个度量连续性的框架,并且通过紧致性等概念,可以进一步研究映射的性质和行为。