参考资料
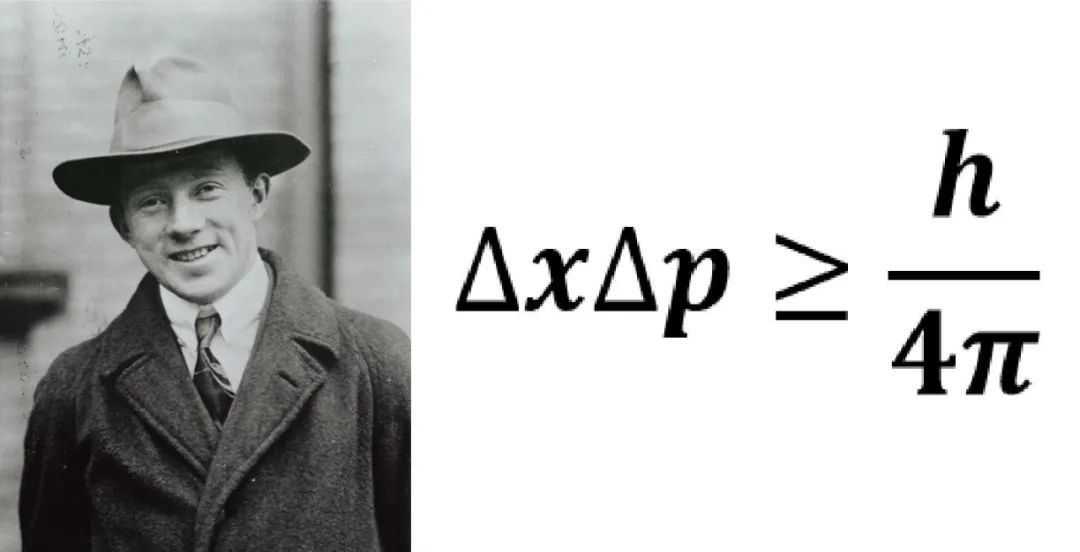

参考资料



Moonshot回答
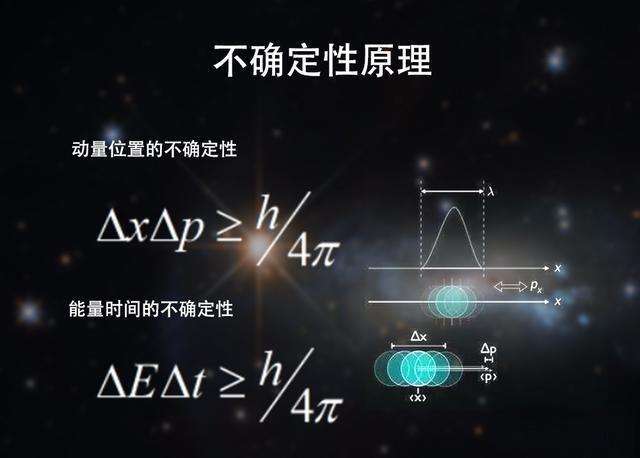
海森堡的不确定性原理自1927年提出以来,在科学界产生了广泛而深远的影响,并在多个领域得到应用。这一原理表明,在量子力学中,无法同时精确测量粒子的位置和动量,从而动摇了经典物理学的决定论基础,并促进了量子力学的发展。它在技术应用上也产生了积极的影响,特别是在如下领域:
-
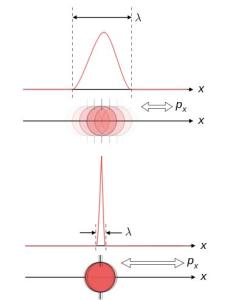
量子力学解释微观世界:不确定性原理深化了我们对量子世界的理解,表明粒子的状态本质上是概率性的。
-
量子计算机和算法设计:在开发量子计算机时,不确定性原理是关键,因为它影响着量子比特(qubits)的设计和操作。
-
材料科学和电子学:在材料科学中,对电子行为的理解可以借助不确定性原理来优化材料的性质,如半导体材料。
-
医学成像技术:例如,在核磁共振成像(MRI)中,对于原子核自旋的测量就涉及到位置和动量的不确定性,科学家通过考虑这一原理来优化图像获取,提高分辨率和准确性。
-
引力波探测:不确定性原理的相关研究有助于发展引力波干涉仪所需的低噪声科技。
不确定性原理不仅在物理学领域内有着基础性作用,还对哲学、认知科学和其他自然科学产生了重要影响。它改变了我们对自然界的认识,推动了科学和哲学的深入探讨。同时,这一原理也是现代科技中许多重要应用的理论基础。通过引用的搜索结果,我们可以看到不确定性原理在科学理论和实际应用中的广泛影响,如参考文献 1、2 和 3 所述。
继续提问
相关问题
为什么土耳其外交官曾威胁美国大屠杀纪念博物馆,如果包含亚美尼亚种族灭绝内容,土耳其可能退出北约?
德涅斯特河沿岸地区急需的医用物资为何无法入境?
波利比乌斯在罗马期间观察了哪些政治制度,并认为它们融合了哪些优点?
阿兹特克文明的研究中,哪些学者的贡献最为突出?
为什么圣墓教堂的管理权会由多个基督教派共同持有,而不是单一教派?
范伟是在哪一年加入沈阳曲艺团从事相声表演的?
茶卡错属于内流区诸河和藏北内流区,这些流域对湖泊的水文环境有哪些具体影响?
阿里巴巴影业集团的第二大股东是哪个女演员及其丈夫,他们持有的股份比例是多少?
麦城之战中,关羽为何最终选择退守麦城?
网站的内容存档方法和作用是什么,为什么重要的网页信息需要存档?