This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe.[23][24] Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.[25]
WMAP[edit]
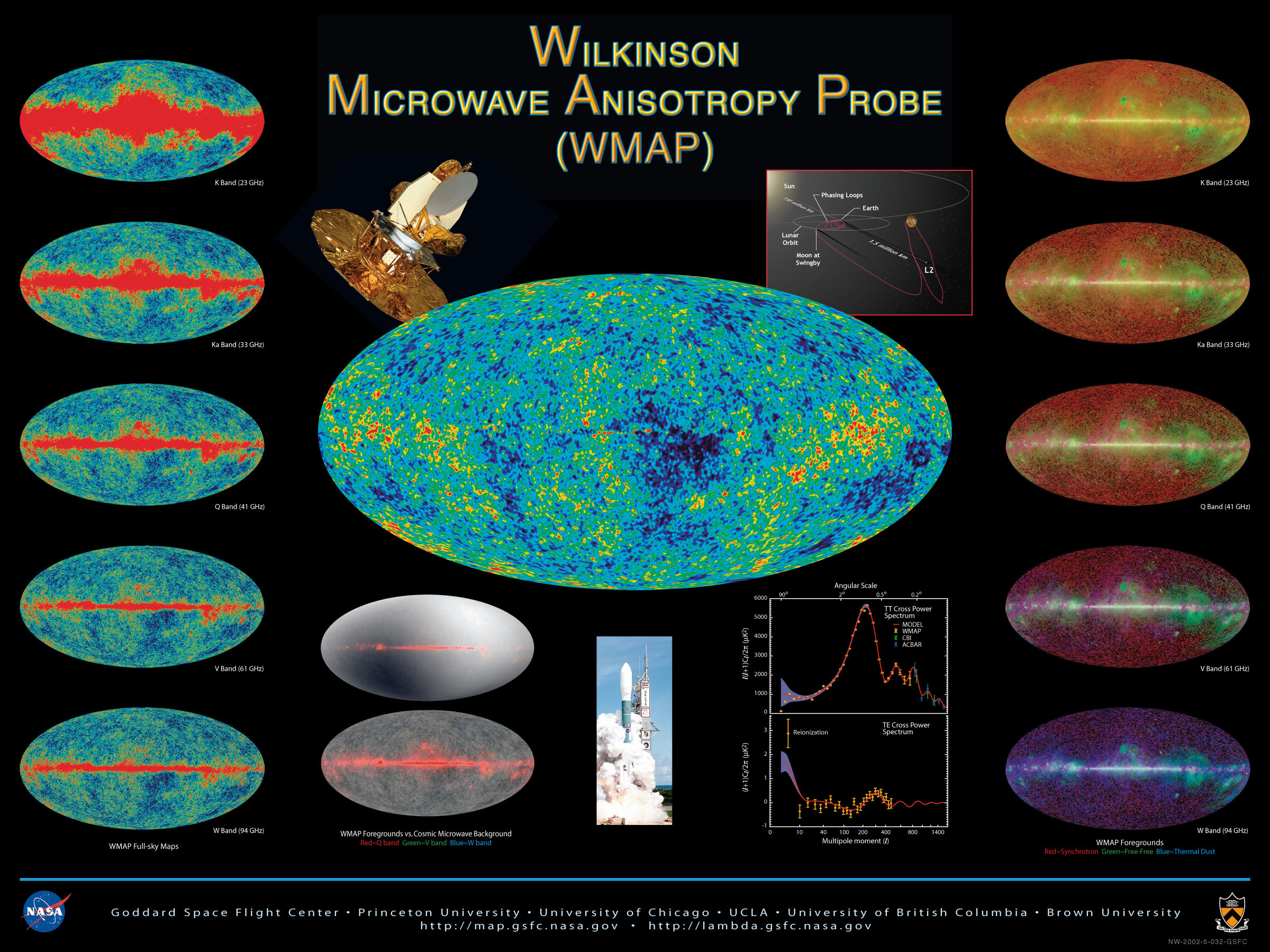
NASA's Wilkinson Microwave Anisotropy Probe (WMAP) project's nine-year data release in 2012 estimated the age of the universe to be (13.772±0.059)×109 years (13.772 billion years, with an uncertainty of plus or minus 59 million years).[6]
This age is based on the assumption that the project's underlying model is correct; other methods of estimating the age of the universe could give different ages. Assuming the validity of the models used to determine this age, the residual accuracy yields a margin of error near one per cent.[13]
Planck[edit]
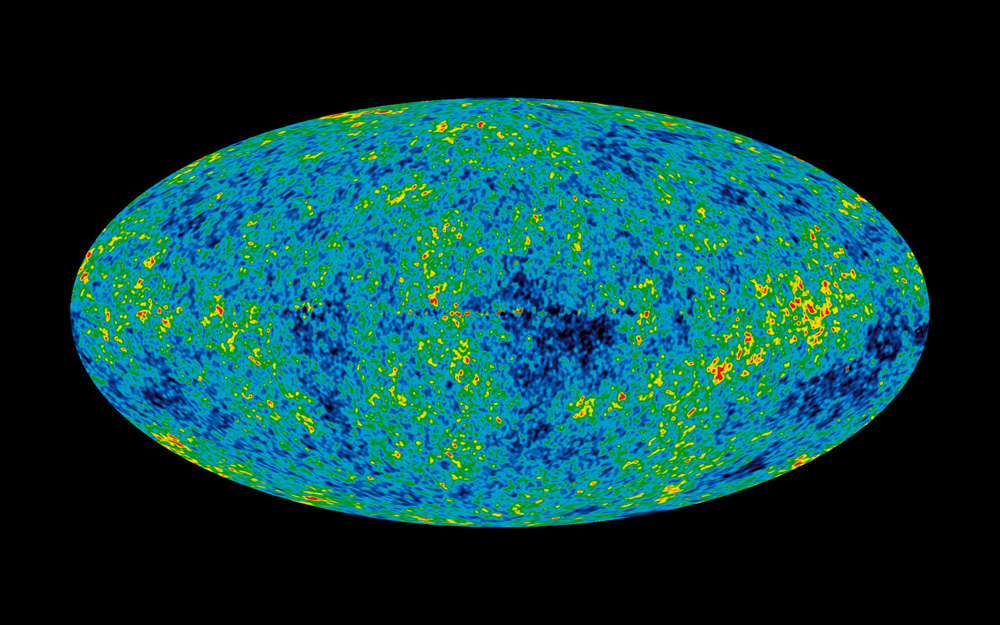
In 2015, the Planck Collaboration estimated the age of the universe to be 13.813±0.038 billion years, slightly higher but within the uncertainties of the earlier number derived from the WMAP data.[27]
The age
t
0
{\displaystyle ~t_{0}~}
is then given by an expression of the form
where
H
0
{\displaystyle ~H_{0}~}
is the Hubble parameter and the function
F
{\displaystyle ~F~}
depends only on the fractional contribution to the universe's energy content that comes from various components. The space probes WMAP, launched in 2001, and Planck, launched in 2009, produced data that determines the Hubble constant and the age of the universe independent of galaxy distances, removing the largest source of error.[13]
Explanation[edit]
The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.77 billion years[14] of cosmological time. Assuming an extra background of relativistic particles, for example, can enlarge the error bars of the WMAP constraint by one order of magnitude.[26]
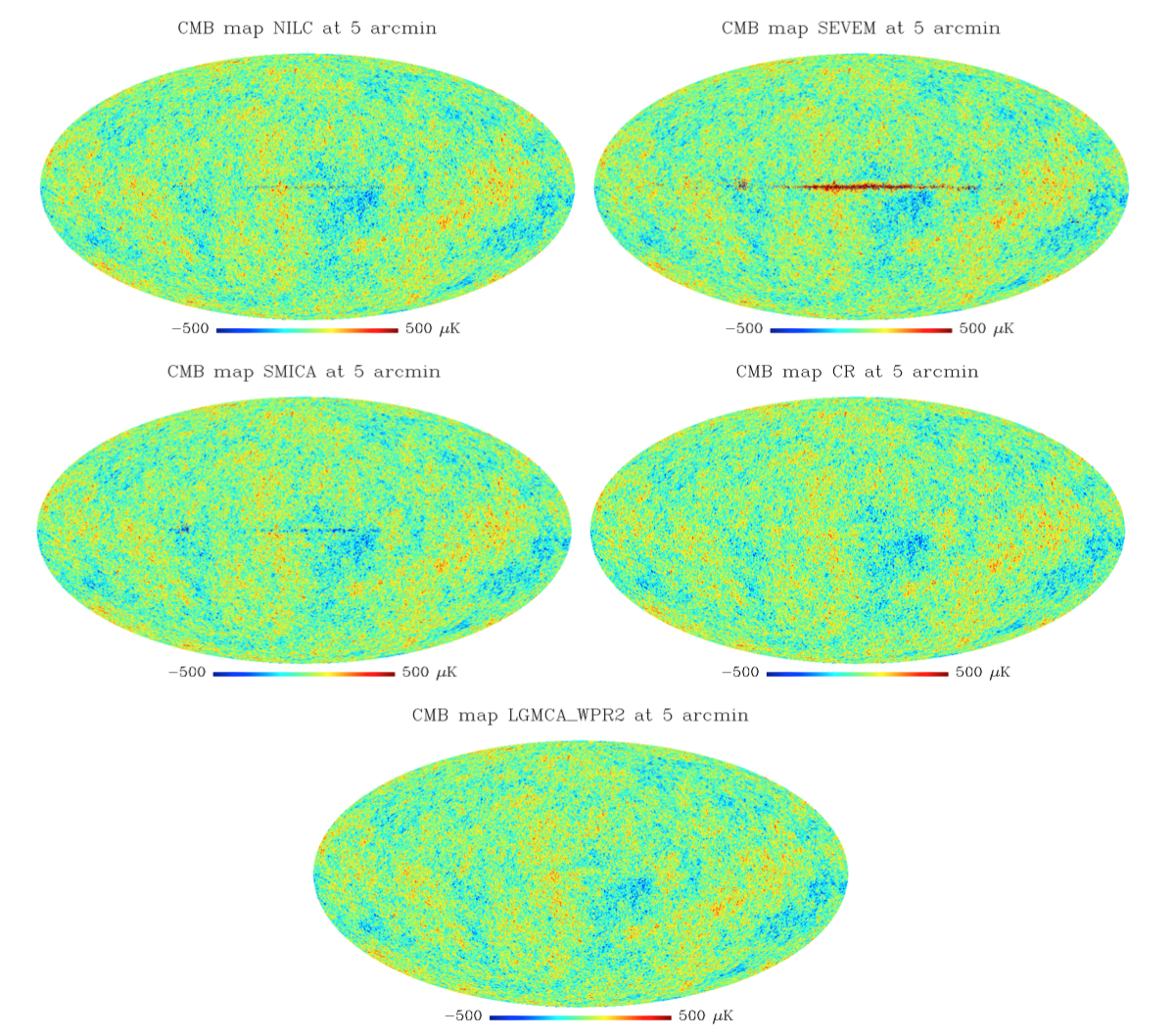
This measurement is made by using the location of the first acoustic peak in the microwave background power spectrum to determine the size of the decoupling surface (size of the universe at the time of recombination).