参考资料
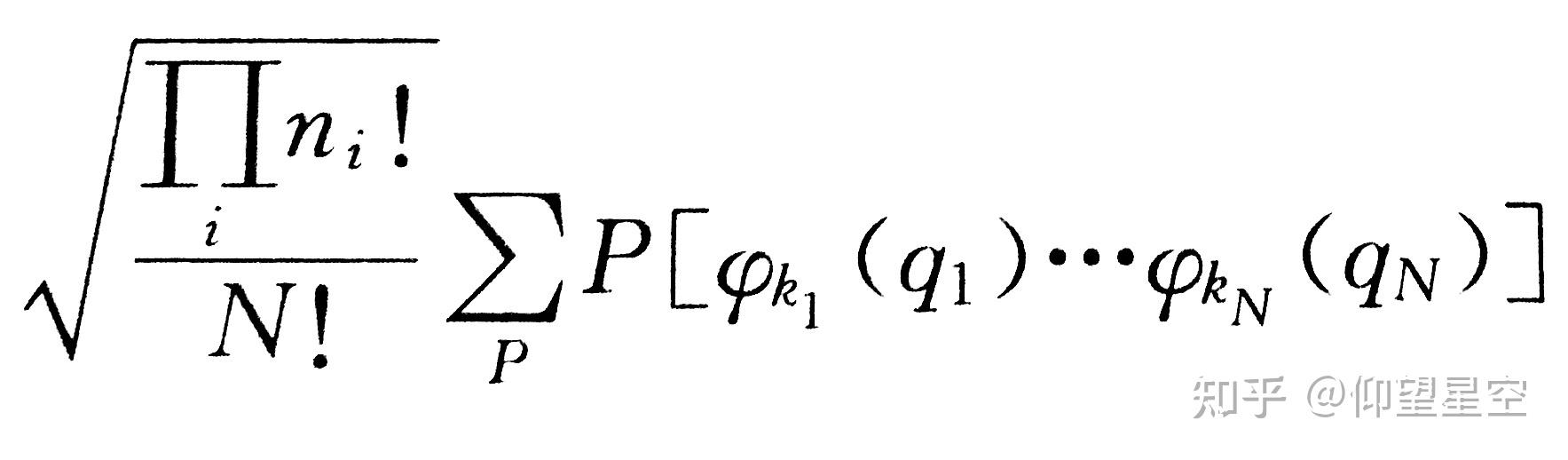
Moonshot回答
斯莱特行列式是量子化学中用于表达多电子体系波函数的一种方法,它以量子物理学家斯莱特的名字命名。这种波函数表达方式可以满足多电子波函数的反对称要求,即泡利原理。根据泡利原理,如果交换体系中任意两个电子的坐标,波函数的符号将会反转。
斯莱特行列式的一般形式如下: [ \Psi(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N) = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_1(\mathbf{r}_1) & \psi_1(\mathbf{r}_2) & \cdots & \psi_1(\mathbf{r}_N) \ \psi_2(\mathbf{r}_1) & \psi_2(\mathbf{r}_2) & \cdots & \psi_2(\mathbf{r}_N) \ \vdots & \vdots & \ddots & \vdots \ \psi_N(\mathbf{r}_1) & \psi_N(\mathbf{r}_2) & \cdots & \psi_N(\mathbf{r}_N) \end{vmatrix} ]
其中,(\psi_i(\mathbf{r}_j)) 表示第 (i) 个单电子波函数在第 (j) 个电子位置 (\mathbf{r}_j) 的值,(N) 是电子的总数。斯莱特行列式通过分子轨道波函数构造,而分子轨道波函数是由体系中所有原子轨道波函数经过线性组合构成的。
在量子化学中,所有基于分子轨道理论的计算方法都用斯莱特行列式来表达多电子体系的波函数。例如,哈特里-福克方法就是使用斯莱特行列式作为多电子波函数的近似表示。
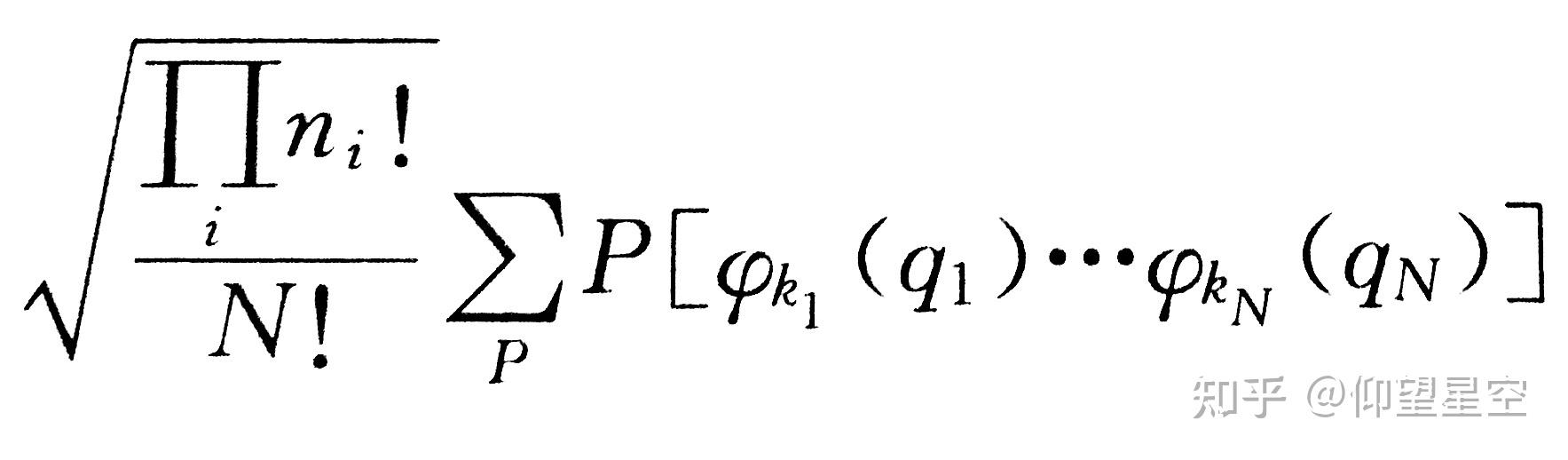 斯莱特行列式图解
斯莱特行列式图解
以上信息参考自百度百科的“库普曼斯定理”、“斯莱特行列式”以及维基百科的相关条目。