何谓马尔可夫链蒙特卡洛方法,它在易辛模型中如何实现?
参考资料
参考资料



Moonshot回答
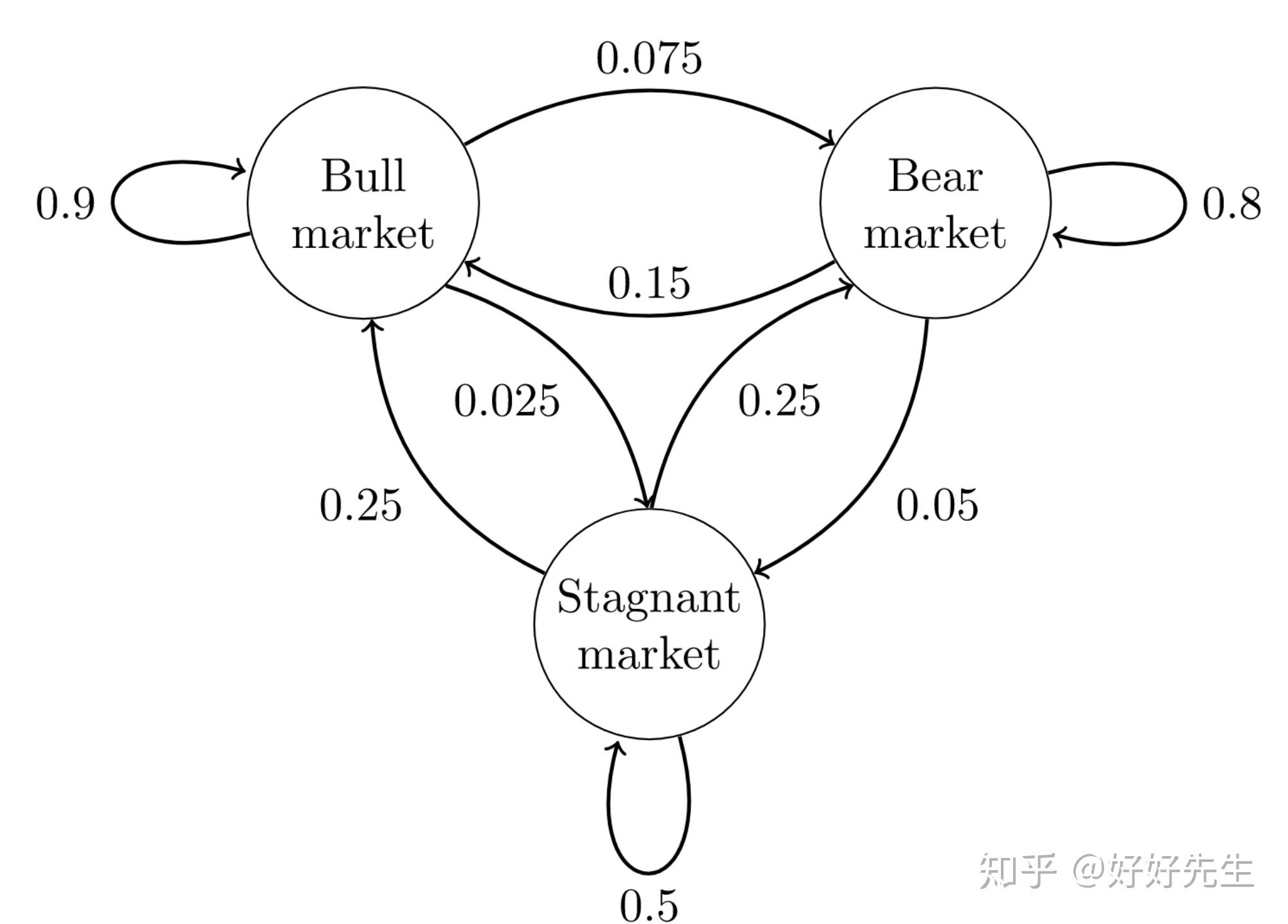
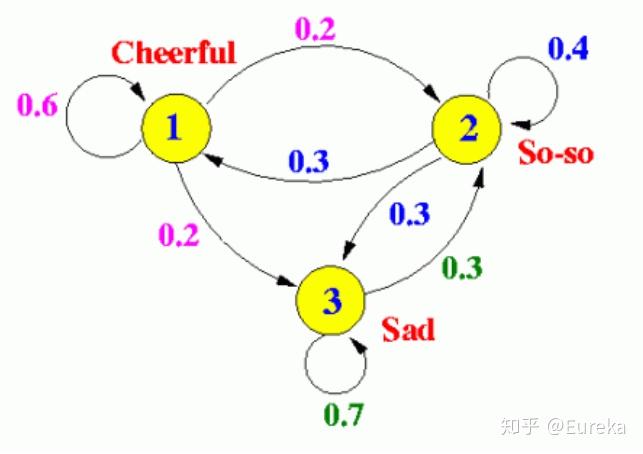
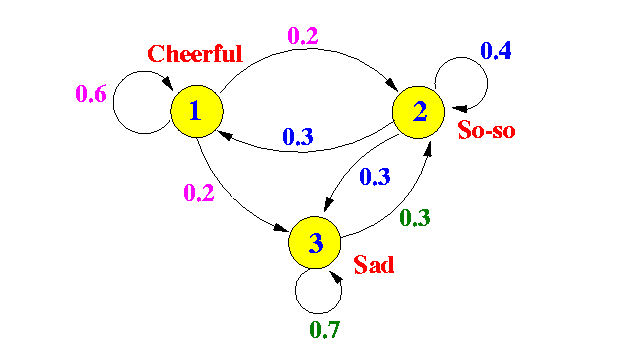
马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法是一种统计学中用于近似复杂分布的算法,它通过构建一个马尔可夫链,使其平稳分布与目标分布相同。在易辛模型中,MCMC方法可以用来模拟系统的磁态,从而研究其相变和临界现象。
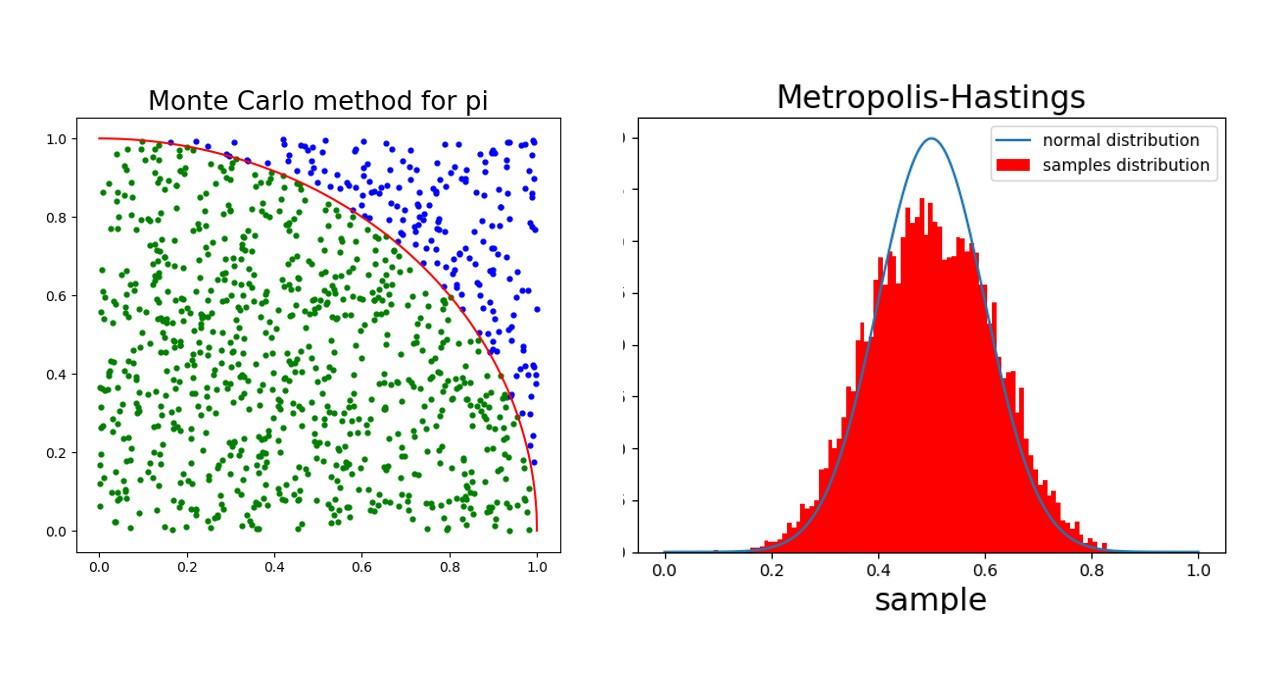
易辛模型是一个数学模型,用于描述铁磁材料中原子磁矩的相互作用。在MCMC方法中,易辛模型的状态可以视为马尔可夫链中的节点,状态转移概率则由系统的哈密顿量和温度决定。通过Metropolis-Hastings算法等,可以从任意初始状态开始,通过随机游走产生一系列状态,最终收敛到目标分布,从而得到系统的热力学性质。
MCMC方法在易辛模型中的应用包括但不限于:
- 估计系统的相变温度和临界指数。
- 研究不同温度和外磁场下的磁化强度和比热容。
- 探索系统的几何结构和拓扑性质。
通过MCMC方法,研究人员可以在易辛模型中进行高效的模拟和分析,从而深入理解其物理行为。这种方法在统计物理、计算生物学和机器学习等领域都有广泛的应用。