经典微积分和现代分析之间的关系,以及它们各自的特点是什么?
参考资料




参考资料


Moonshot回答
经典微积分和现代分析学都是数学中的重要分支,它们之间存在密切的联系,同时也各有特点。
经典微积分主要研究函数的极限、导数、积分等概念,其特点包括:
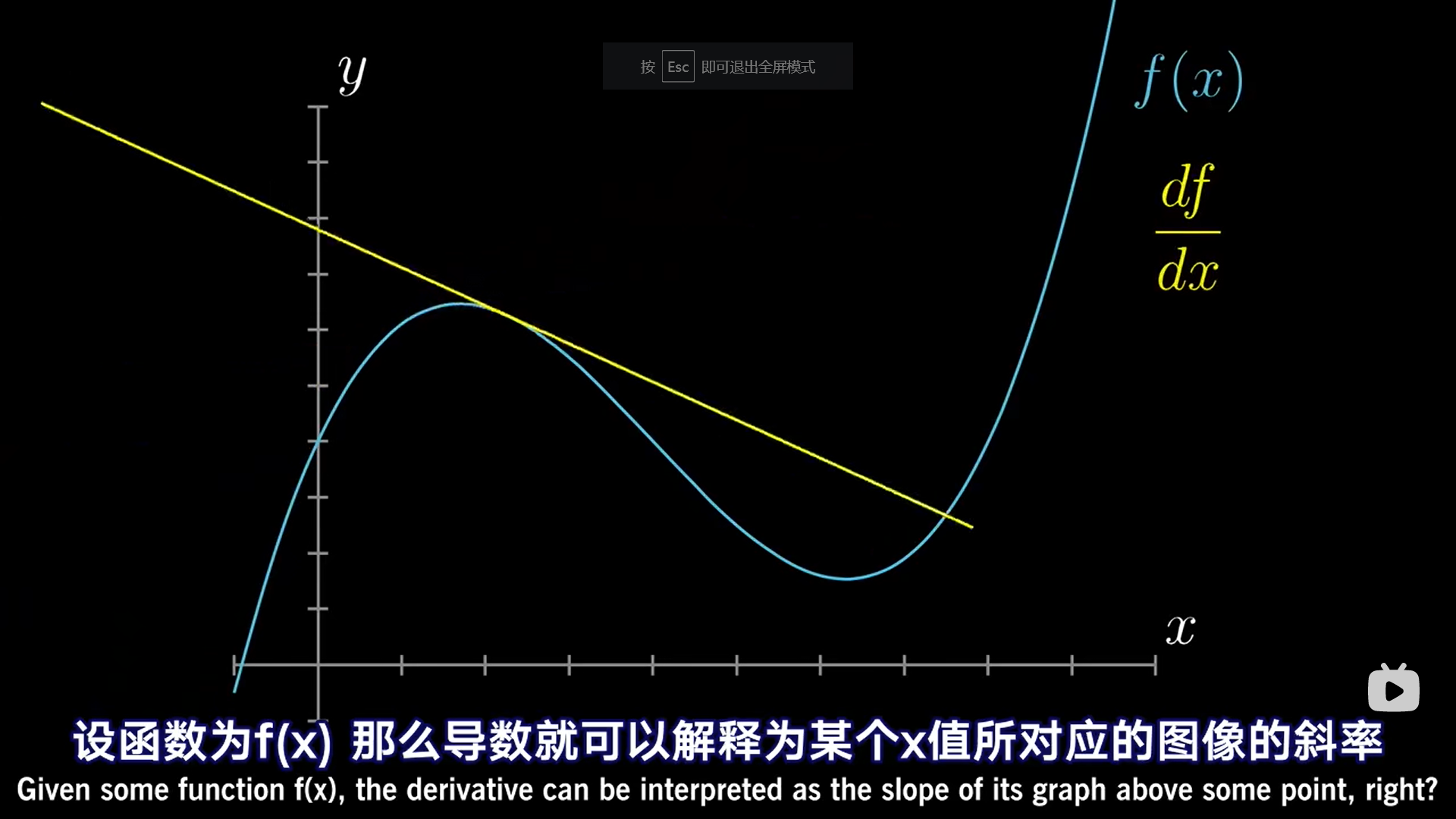
- 连续性:函数在某一点的极限值等于该点的函数值,保证了函数图像的平滑过渡。
- 微分性:研究函数在某一点的局部变化率,即导数。
- 积分性:研究函数在某个区间上的累积变化,即积分。 经典微积分以极限概念为核心,建立在实体无穷小量的假设之上,强调直观和计算,适用于解决物理学、工程学等领域的问题。
现代分析学则在此基础上进一步发展,特点包括:
- 严谨性:使用集合论、拓扑学等数学工具,对微积分的概念和方法进行严格定义和证明。
- 泛化性:将微积分的概念推广到更一般的数学对象上,如泛函分析、流形上的分析等。
- 应用广泛:现代分析学不仅用于传统的科学领域,还扩展到经济学、生物学等新兴领域。 现代分析学的发展特别吸收和利用了集合论、代数以及拓扑的思想和方法,涉及的专业面越来越广。
总的来说,经典微积分为现代分析学的发展奠定了基础,而现代分析学则在经典微积分的基础上进行了严格的理论化和泛化,两者相辅相成,共同推动了数学及其它科学领域的发展。