广义相对论中的度规张量是什么,它在描述空间几何时起什么作用?
参考资料

Moonshot回答
在广义相对论中,度规张量是一个描述时空几何的基本数学对象。它是一个对称的二阶张量,用于测量时空中两点之间的距离和角度。度规张量定义了时空的曲率,并且通过它我们可以计算出两点之间的间隔,进而了解时空的几何结构。
度规张量在广义相对论中的作用主要体现在以下几个方面:
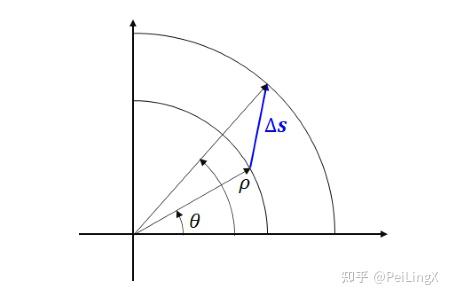
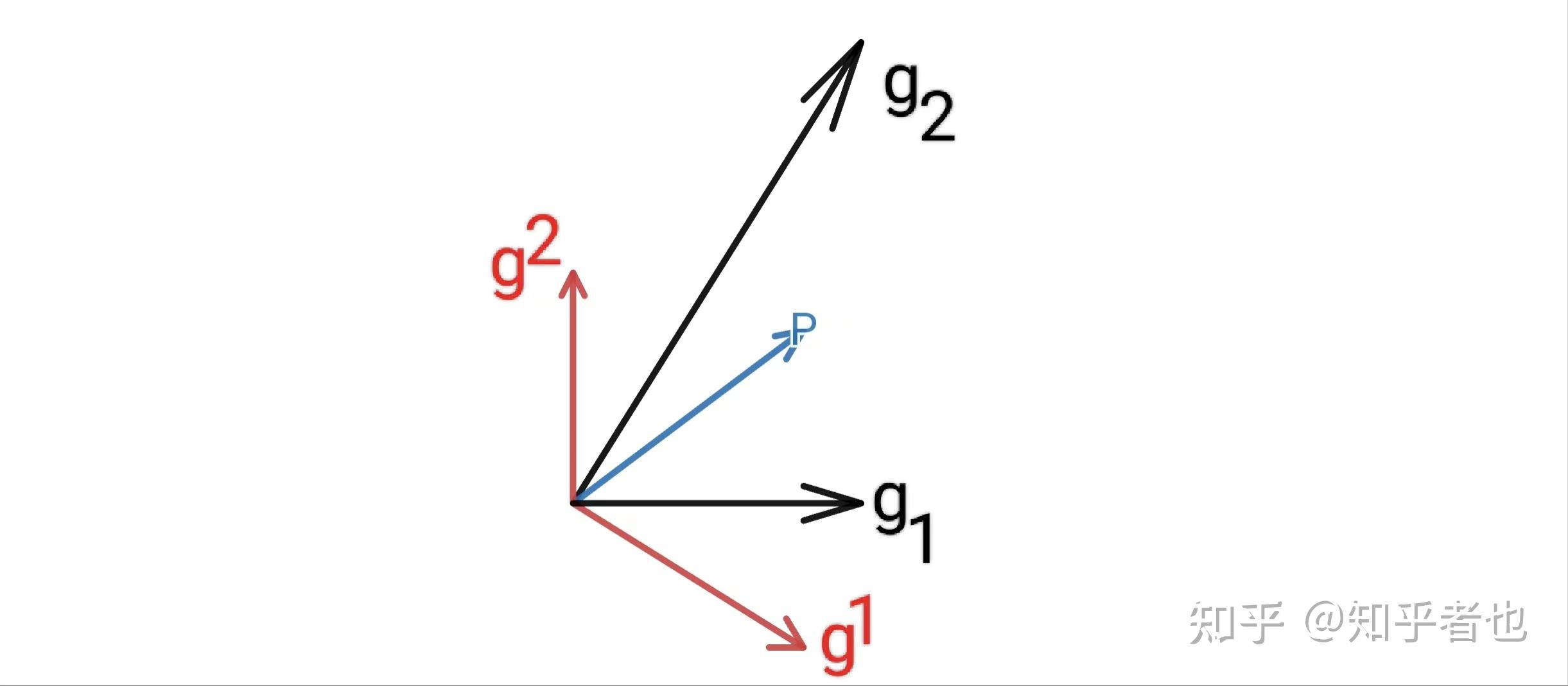
- 定义时空间隔:度规张量允许我们计算任意两点之间的时空间隔,这是理解时空几何的基础。
- 描述时空曲率:通过度规张量,我们可以了解时空如何被物质和能量所弯曲。
- 构建测地线:在弯曲的时空中,度规张量帮助我们找到两点间的最短路径,即测地线,这在研究天体运动时非常重要。
- 导出场方程:在广义相对论中,爱因斯坦场方程是通过度规张量和物质的能量-动量张量联系起来的,描述了物质如何影响时空的几何。
此外,广义相对论的实验验证,例如光线在强引力场中的偏转、引力时间膨胀等现象,都与度规张量有着密切的关系。通过研究度规张量,科学家们能够更深入地理解宇宙的运作原理,包括黑洞和宇宙大爆炸理论。
 图片来源:知乎专栏
图片来源:知乎专栏