Metropolis算法的基本流程是怎样的？
参考资料
Moonshot回答
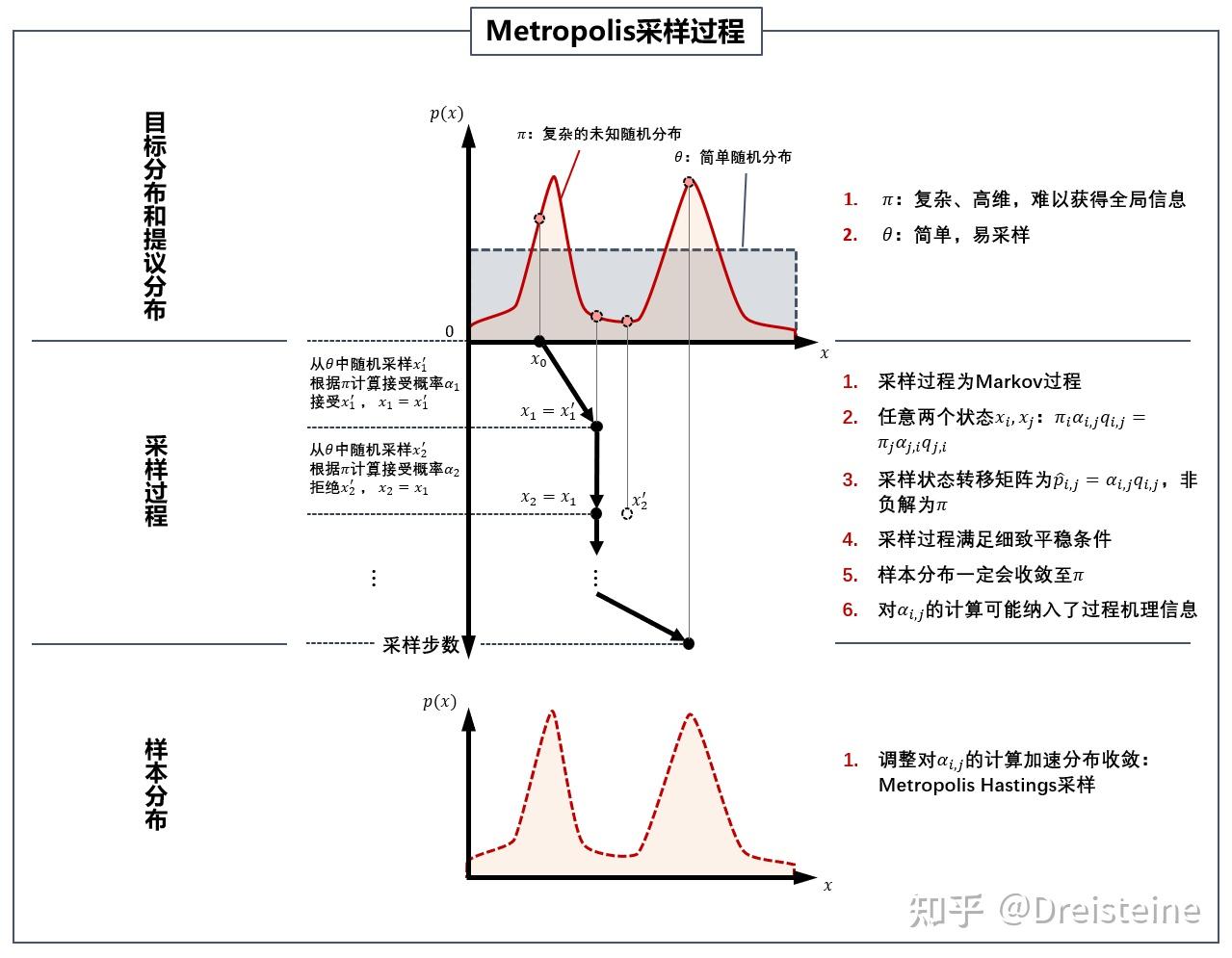
Metropolis算法的基本流程如下：
- 初始化：选择一个初始状态 ( x_0 ) 并计算其对应的能量 ( E(x_0) )。
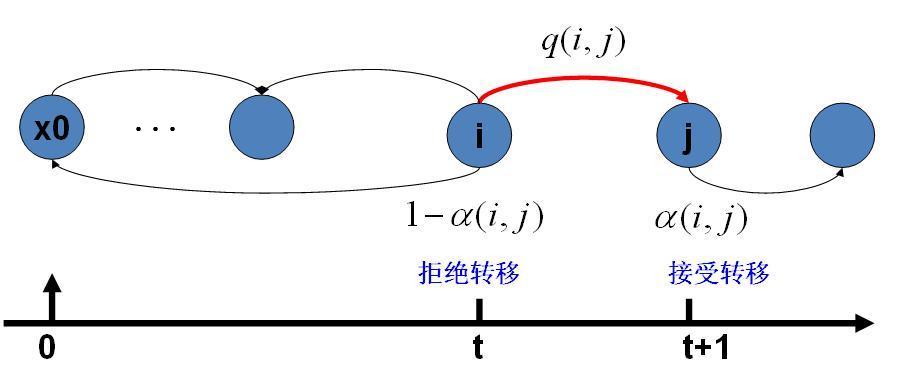
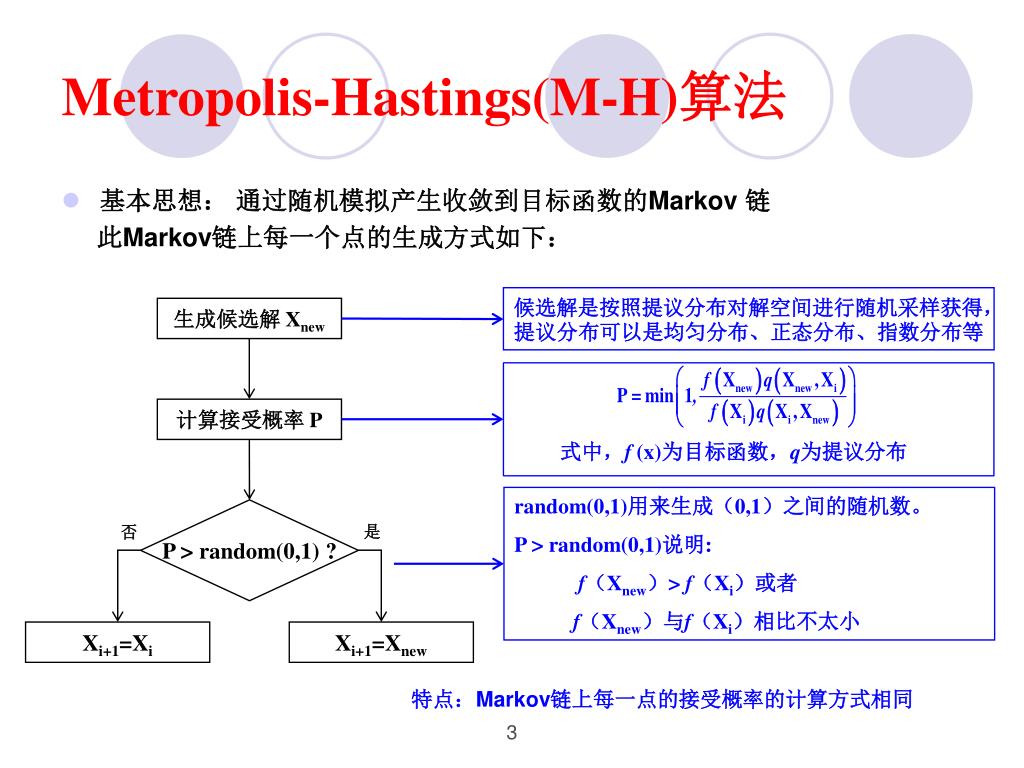
- 生成候选状态：在当前状态 ( x_t ) 的基础上，随机产生一个候选状态 ( x' )。这通常通过在当前状态上施加小的扰动来实现。
- 计算接受概率：计算从当前状态 ( x_t ) 转移到候选状态 ( x' ) 的接受概率 ( A )。如果 ( E(x') \leq E(x_t) )，则接受概率为1；如果 ( E(x') > E(x_t) )，则接受概率为 ( \min\left(1, \exp\left(-\frac{E(x') - E(x_t)}{kT}\right)\right) )，其中 ( k ) 是玻尔兹曼常数，( T ) 是温度。
- 决定是否接受：以计算出的接受概率 ( A ) 为依据，通过生成一个0到1之间的随机数 ( r ) 来决定是否接受候选状态。如果 ( r < A )，则接受 ( x' ) 作为下一个状态；否则，保持当前状态不变。
- 迭代：重复步骤2到4，直到满足收敛条件或达到预定的迭代次数。
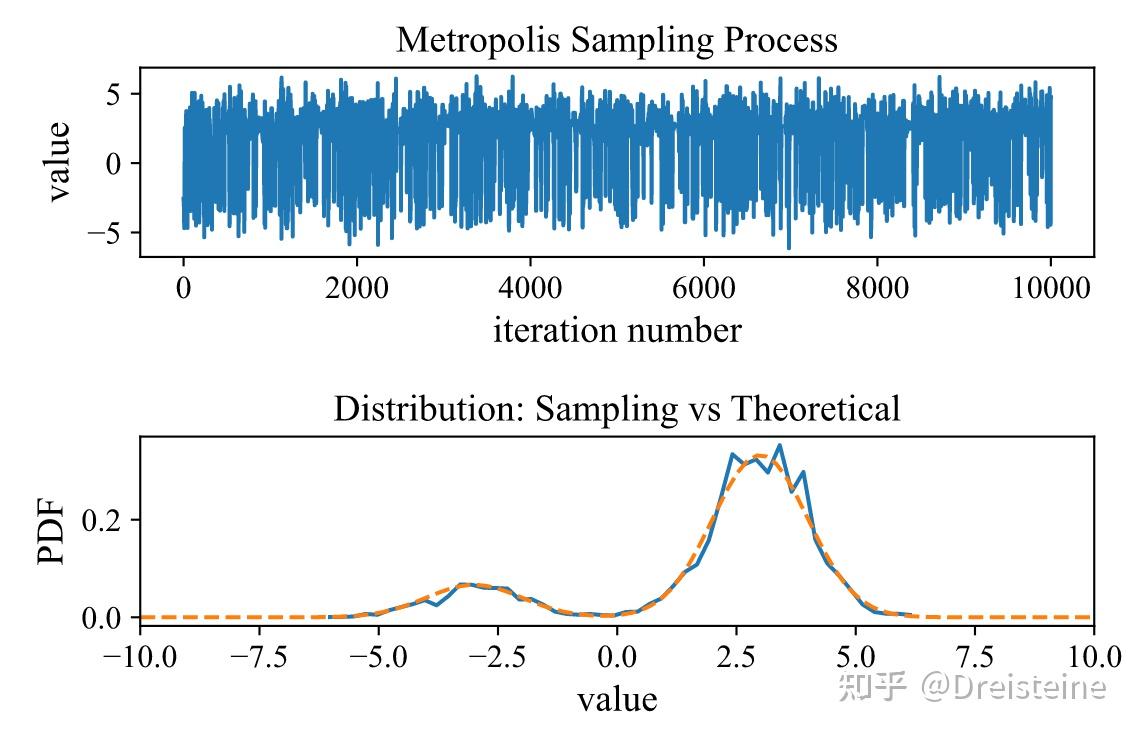
Metropolis算法是马尔可夫链蒙特卡洛（MCMC）方法的特例，它通过构建一个马尔可夫链来从目标分布中抽取样本。该算法在统计物理、计算生物学、机器学习等领域有广泛应用。
图片展示了Ising模型的Monte Carlo模拟过程，其中Metropolis算法是核心步骤之一。图片来源：知乎专栏文章《Ising 模型的 Monte Carlo模拟》。