平移算符在量子力学中的作用是什么?
参考资料
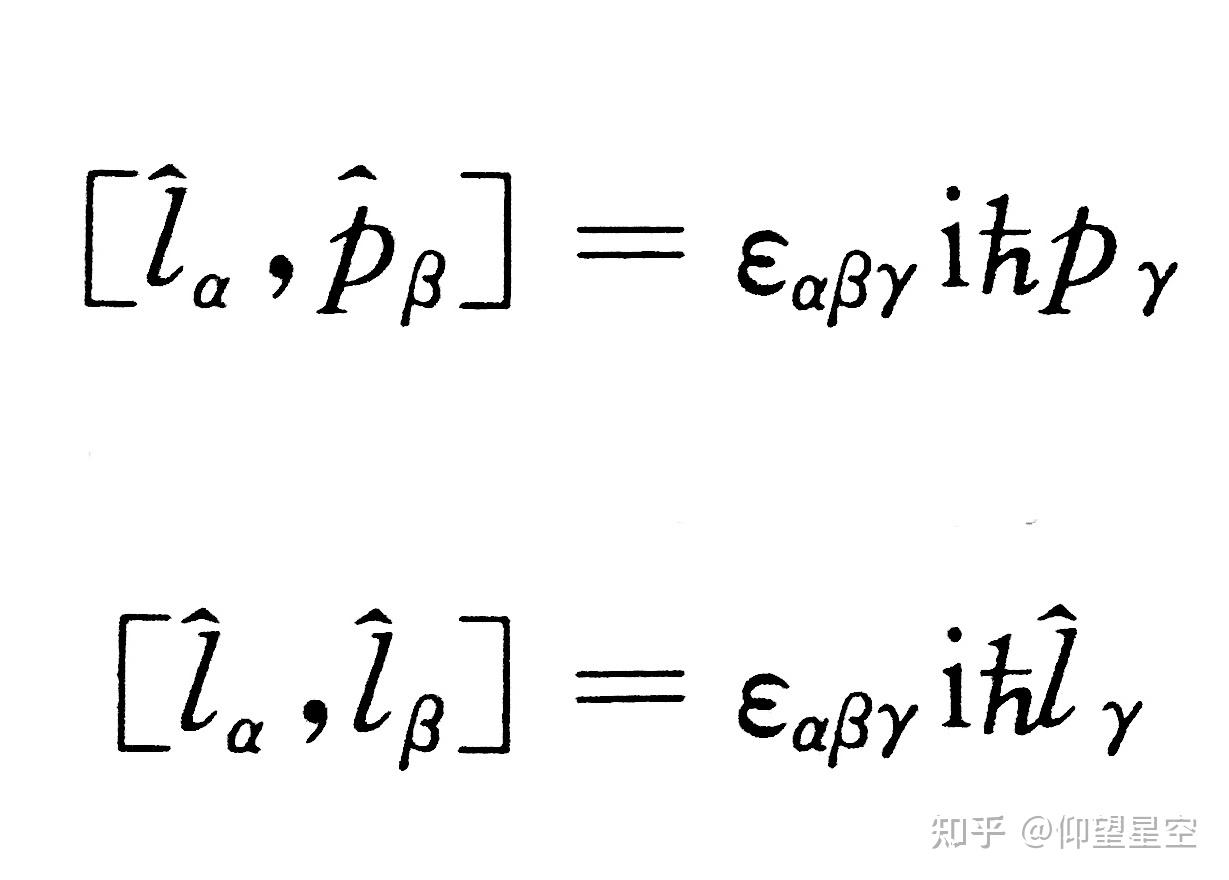

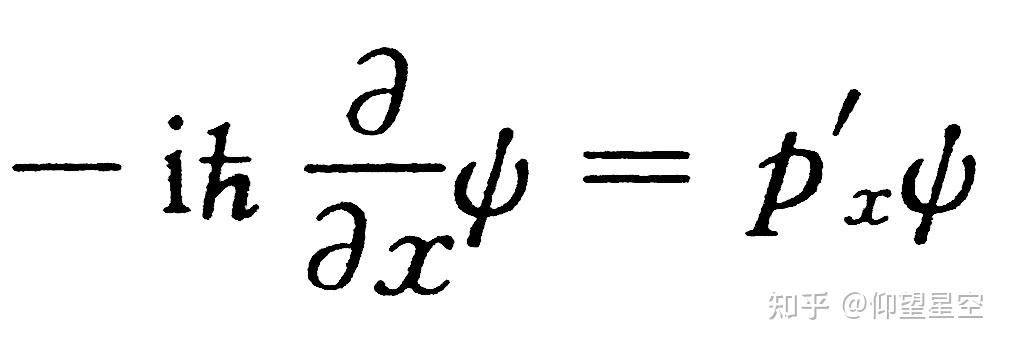
Moonshot回答
在量子力学中,平移算符扮演着至关重要的角色。它用于描述量子态在空间中的平移,而不会改变其物理性质。具体来说,平移算符的主要作用包括:
-
实现量子态的空间平移:平移算符可以将一个量子态从一个位置平移到另一个位置。例如,算符( T(a) )作用在状态( \ket{x} )上,会得到( \ket{x+a} ),表示状态的空间平移。
-
与动量算符的关系:平移算符和动量算符之间存在基本的对易关系。这种关系揭示了空间平移与动量之间的深刻联系,是量子力学中的一个重要概念。
-
对称性和守恒定律:平移对称性是量子力学中的一个基本原理,它导致了物理定律在空间平移下的不变性。根据诺特定理,这种对称性对应于动量的守恒。
-
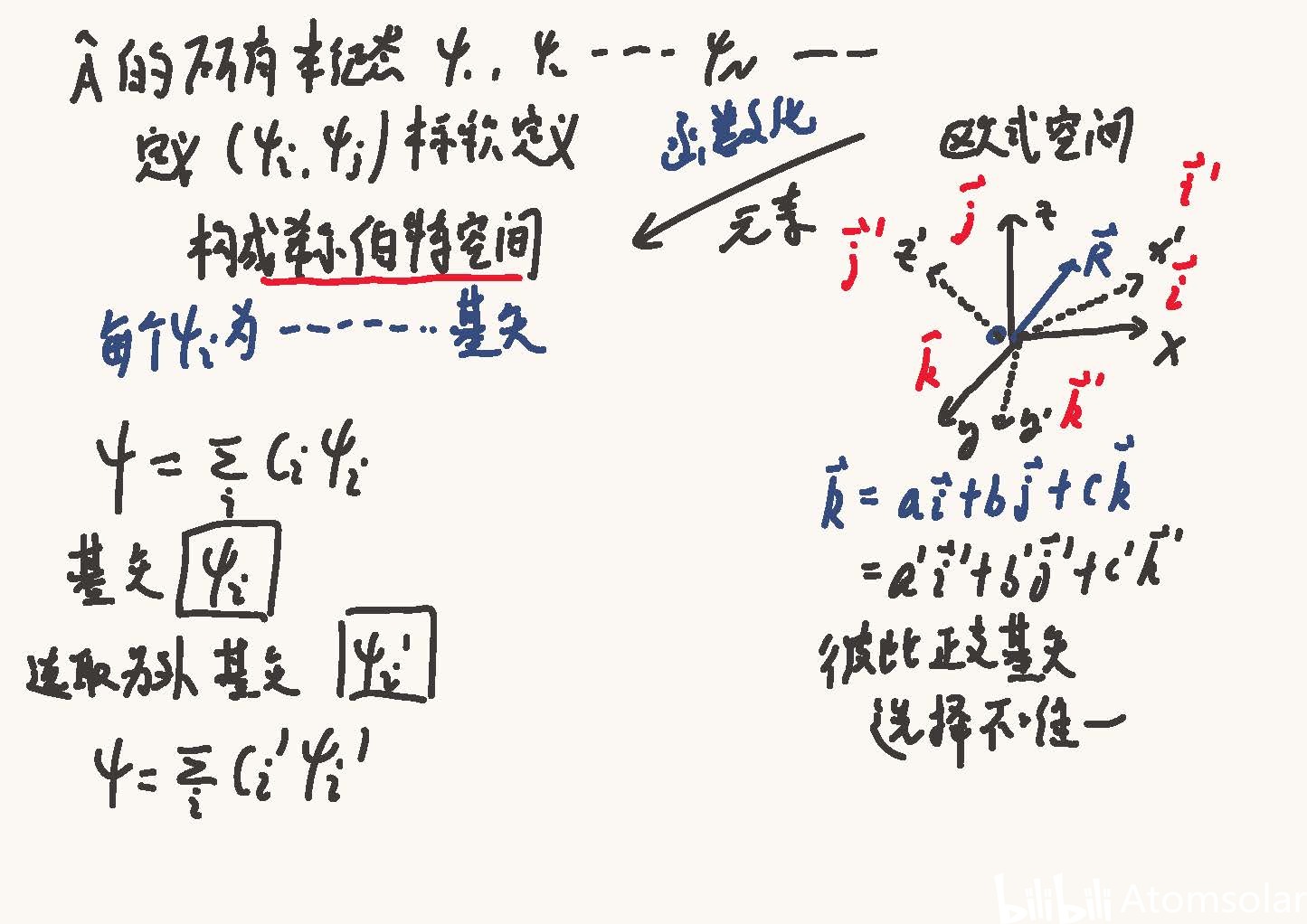
量子态的变换:平移算符可以用来描述量子态在不同位置本征态之间的变换,这对于理解量子系统的动力学行为至关重要。
通过引用的搜索结果,我们可以看到平移算符在量子力学中的作用是多方面的,它不仅涉及到量子态的空间平移,还与动量算符的对易关系、对称性和守恒定律以及量子态的变换紧密相关。这些概念是理解量子力学的基础,对于研究量子系统的行为至关重要。