在格拉德-沙夫拉诺夫方程中,如何定义和计算磁场矢量?
参考资料

参考资料


Moonshot回答
格拉德-沙夫拉诺夫方程是用于描述理想等离子体中磁场和等离子体压强分布的一个方程。在该方程中,磁场矢量的定义和计算如下:
-
定义:格拉德-沙夫拉诺夫方程中,磁场矢量通常用符号 (\mathbf{B}) 表示,并且是等离子体中的一个重要物理量。它与电流密度 (\mathbf{J}) 通过安培定律相关联,即 (\nabla \times \mathbf{B} = \mu_0 \mathbf{J}),其中 (\mu_0) 是真空的磁导率。
-
计算:在格拉德-沙夫拉诺夫方程中,磁场矢量 (\mathbf{B}) 可以通过求解该方程得到。方程的一般形式为: [ \frac{1}{R}\frac{\partial}{\partial R}\left(R B_\theta\right) + \frac{1}{R^2}\frac{\partial B_z}{\partial z} = \frac{\mu_0}{q} \frac{\partial p}{\partial s} ] 其中,(R) 是柱坐标系中的径向距离,(B_\theta) 和 (B_z) 分别是磁场在 (\theta) 和 (z) 方向上的分量,(p) 是等离子体压强,(s) 是沿磁场线的坐标,(q) 是安全因子。
-
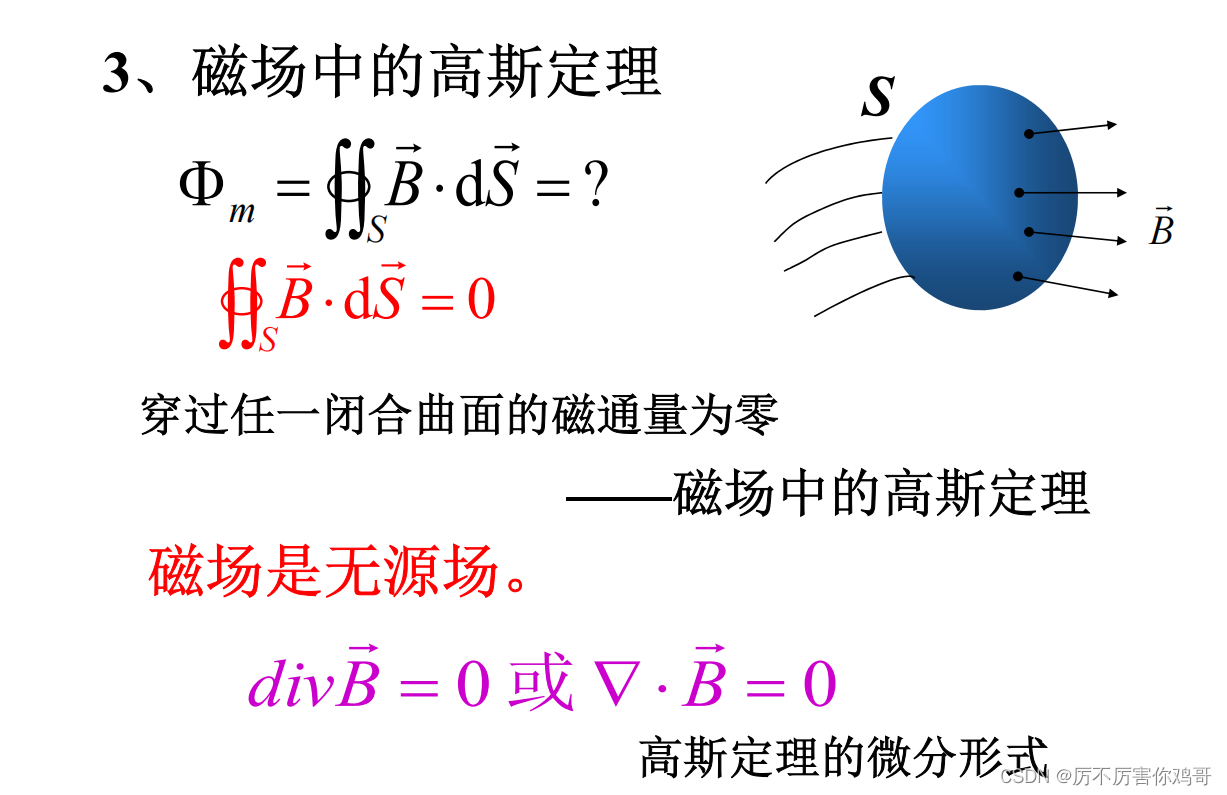
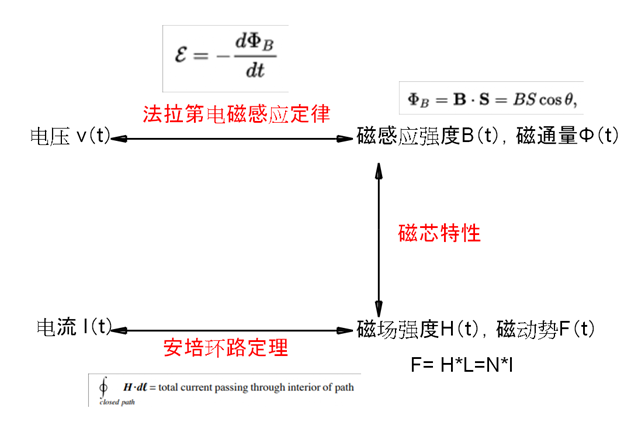
图像:搜索结果中提供了一些与格拉德-沙夫拉诺夫方程相关的图像,这些图像有助于直观理解磁场矢量在等离子体中的分布情况。例如,一张图片展示了等离子体中磁场线的形状,另一张图片则展示了磁场矢量与等离子体压强之间的关系。
通过求解格拉德-沙夫拉诺夫方程,可以计算出磁场矢量在等离子体中的分布情况,这对于研究和设计受控核聚变装置等具有重要意义。更多详细信息可以参考维基百科上的格拉德-沙夫拉诺夫方程条目。