参考资料



参考资料


Moonshot回答
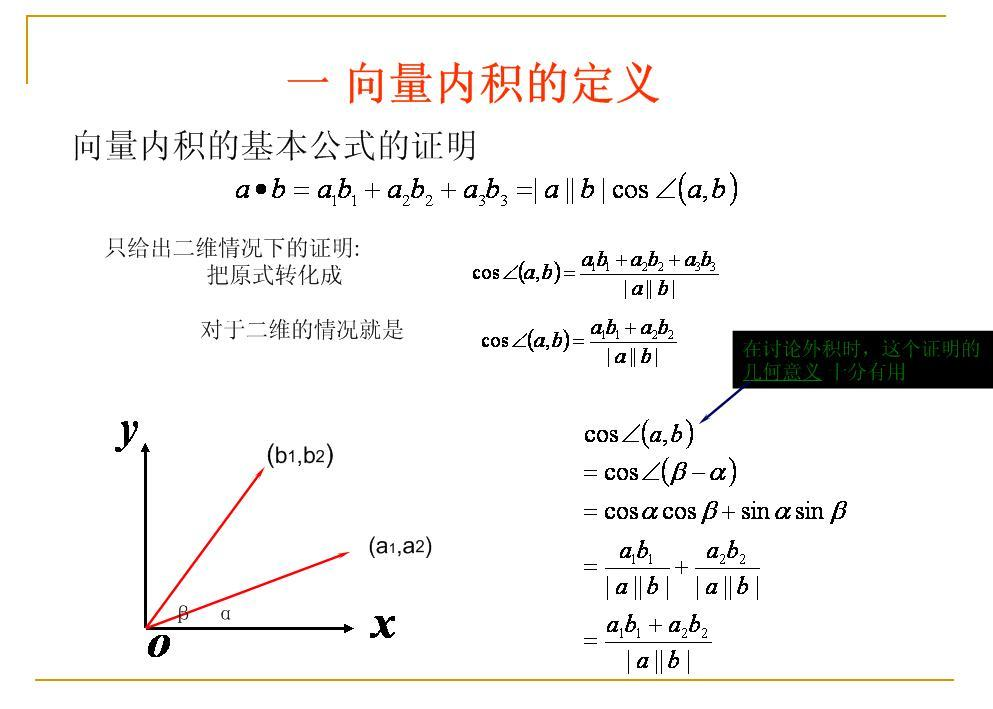
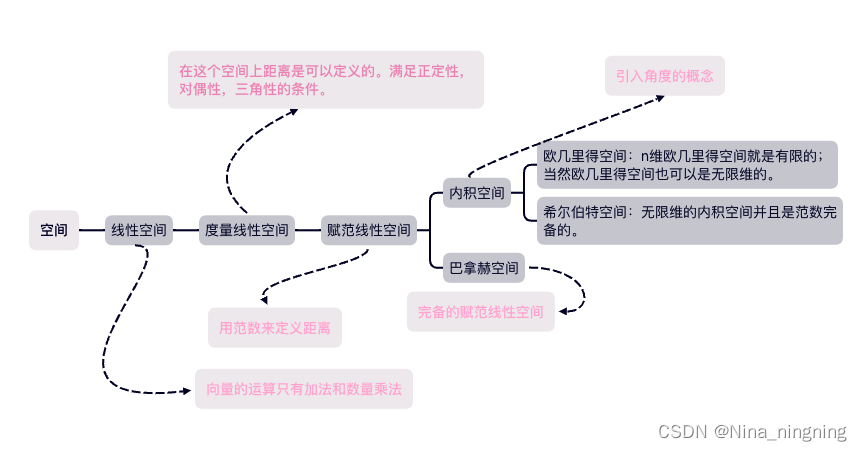
内积是一种双线性函数,它在不同的函数空间中可能有不同的定义。例如,在函数空间中,内积可以用积分或序列来表示,而在欧几里得空间中,内积通常指的是点积。内积空间有时也被称为准希尔伯特空间,因为由内积定义的距离完备化之后会得到一个希尔伯特空间。
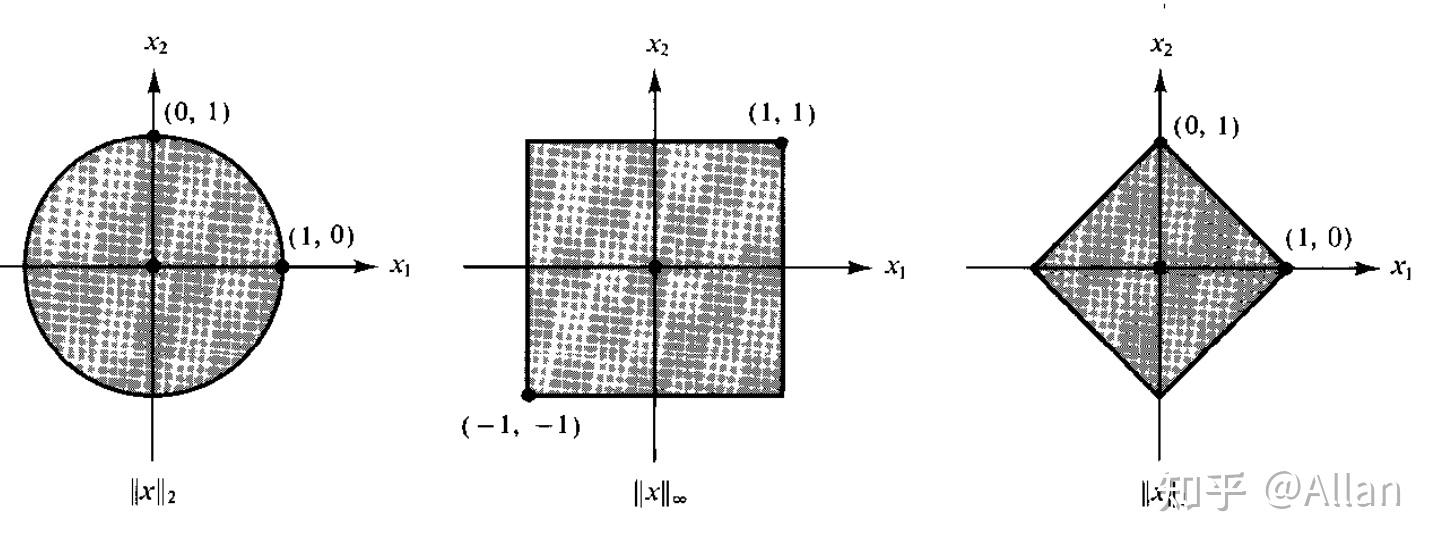
内积与欧几里得范数之间存在密切的关系。在内积空间中,内积可以用来定义范数,即一个向量的欧几里得范数可以通过它与自身的内积的平方根来计算。具体来说,对于一个向量 ( \mathbf{v} ),其欧几里得范数定义为 ( |\mathbf{v}| = \sqrt{\langle \mathbf{v}, \mathbf{v} \rangle} ),其中 ( \langle \mathbf{v}, \mathbf{v} \rangle ) 表示向量 ( \mathbf{v} ) 与其自身的内积。
此外,内积空间中的平行四边形法则也与欧几里得范数有关,该法则表明两个向量的和与差的欧几里得范数的平方和等于它们各自欧几里得范数平方和的两倍。
 图片展示了内积与欧几里得范数的关系。
图片展示了内积与欧几里得范数的关系。
通过以上信息,我们可以看到内积在定义欧几里得范数和构建内积空间中起着核心作用。内积不仅可以用来测量两个向量之间的夹角,还可以用来定义正交函数和正交空间,是线性代数和泛函分析中的重要概念。
继续提问
相关问题
勒·西夫在2006年电影《007:大战皇家赌场》中的结局是怎样的,他是被谁杀死的?
亚美尼亚是世界上第一个将基督教定为国教的国家,这一历史事件发生在哪一年?
拜占庭帝国的利奥三世为何被称为“破坏圣像者”?
什切青的交通网络是如何构成的?
幼圆体与其他圆体字体相比,有哪些独特的设计特点?
理查·麦克哥纳尔的配音角色中,哪一个角色是《超人特攻队》中的超能先生?
格拉纳达酋长国是如何成为伊比利亚半岛上最后一个伊斯兰国家的?
《座头市凶状旅》是“座头市系列”的第几部电影,这一系列的前作和续作分别是什么?
《拉贝日记》电影的制片预算是多少,这部电影的制作成本是否物有所值?
为什么《启程的日子》最终能够替代传统的毕业歌曲成为主流?