什么是希尔伯特空间中的自同构,为什么幺正算符也是自同构?
参考资料

参考资料
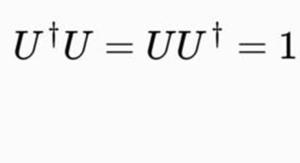



Moonshot回答
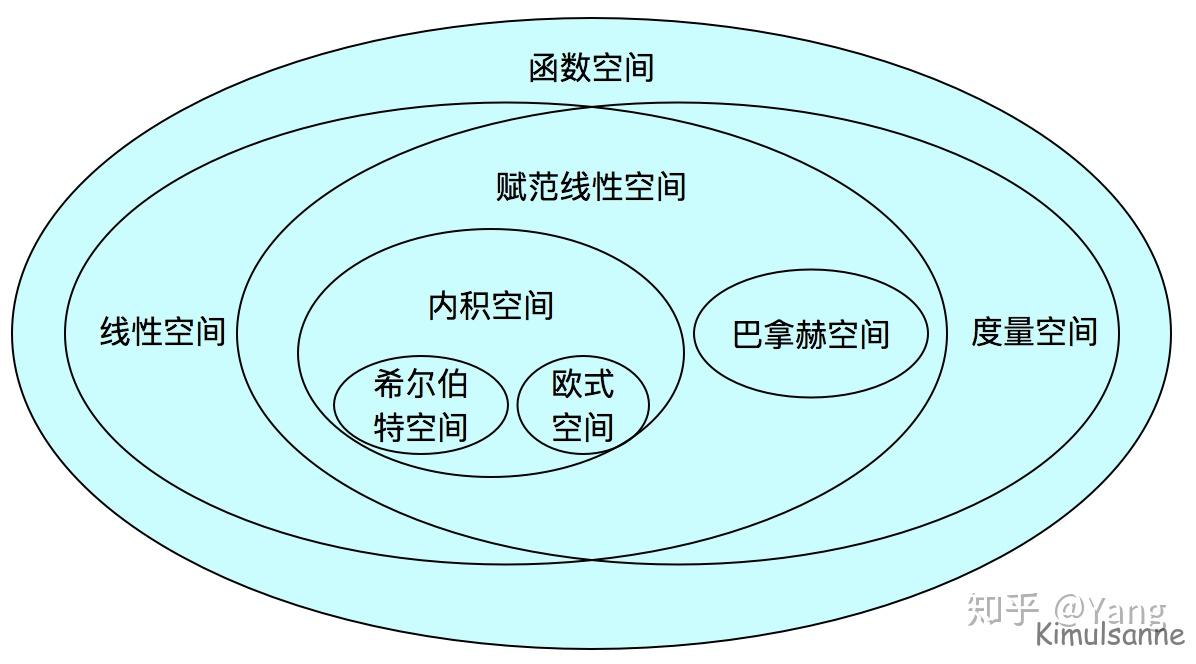
希尔伯特空间中的自同构是指一个从空间到其自身的双射线性映射,它保持了空间的内积结构,即保持了向量的范数和内积不变。这意味着自同构映射不仅保持了向量的长度和它们之间的角度,还保持了空间的拓扑结构。
幺正算符是希尔伯特空间上的一类特殊的线性算子,它们满足保持内积不变的性质。具体来说,对于任意两个向量( u )和( v ),有( \langle Uu, Uv \rangle = \langle u, v \rangle ),其中( U )是幺正算符。这表明幺正算符不仅保持了向量的长度,还保持了它们之间的角度,因此也保持了空间的拓扑结构。
根据搜索结果,幺正算符是希尔伯特空间的自同构,因为它们保持了空间的线性叠加性和内积以及拓扑性质的不变[1]。在群论中,一个给定希尔伯特空间H上的所有幺正算符组成了该空间的希尔伯特群,表示为Hilb(H)[2]。这进一步说明了幺正算符作为自同构的性质,因为群论中的自同构是保持群结构的双射同态,而幺正算符正是这样的映射。
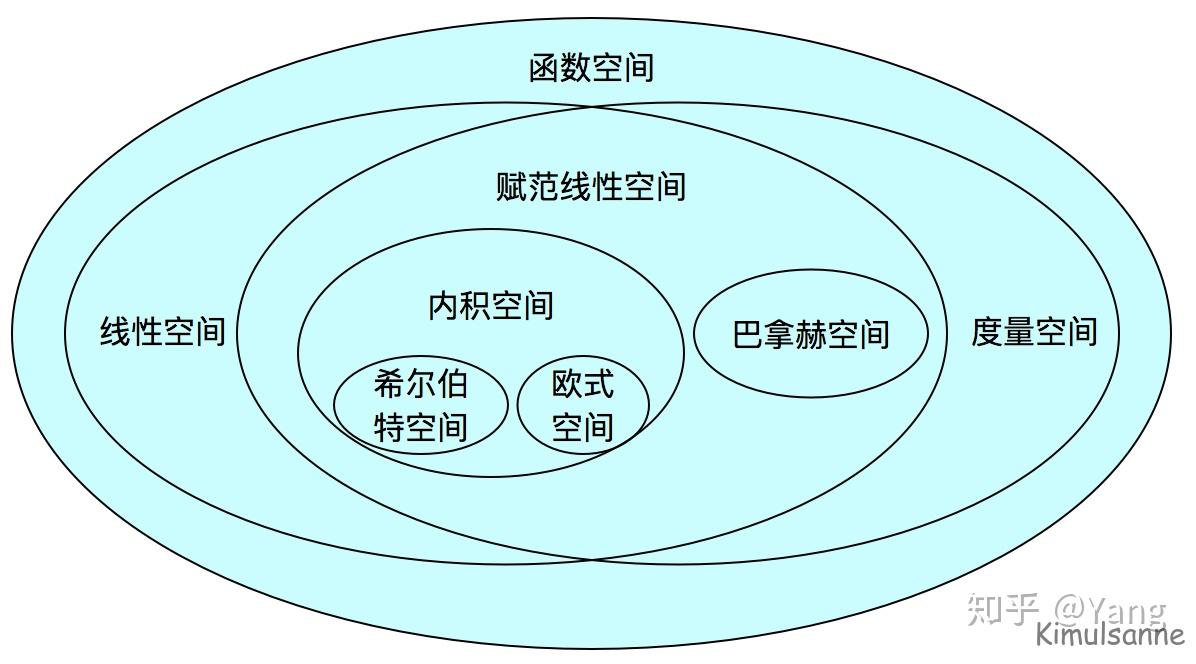
这张图片展示了希尔伯特空间的概念,其中包含了自同构和幺正算符的性质。
引用来源: [1] 幺正算符 - 维基百科,自由的百科全书: https://zh.wikipedia.org/wiki/幺正算符 [2] 如何通俗的解释希尔伯特空间,它具有特别的性质么,如果有是什么? - 知乎: https://www.zhihu.com/question/27898379