如何通过格拉姆-施密特正交化过程找到向量空间中的正交基？
参考资料
Moonshot回答
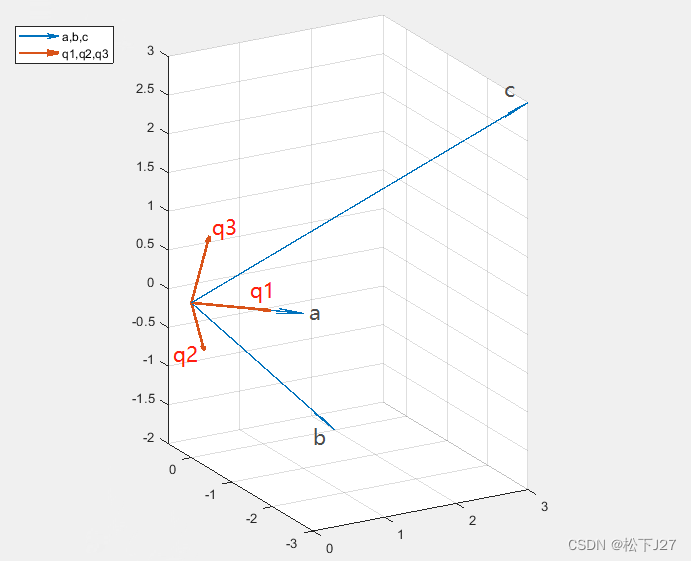
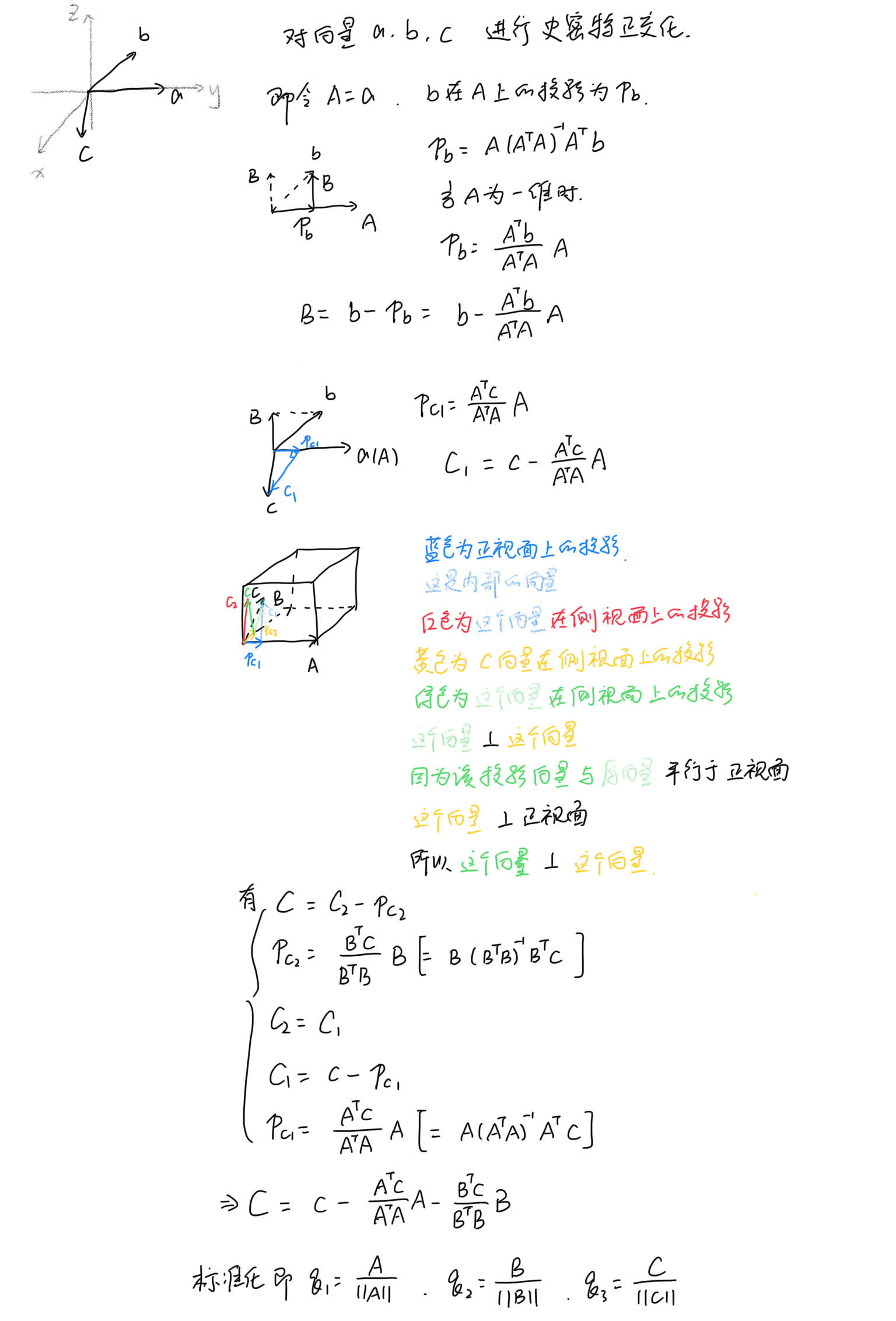
格拉姆-施密特正交化过程是一种在内积空间中，通过一组线性无关的向量集合来生成一组正交或标准正交基的方法。以下是该过程的步骤：
- 从一个线性无关的向量集合 ({v_1, v_2, ..., v_n}) 开始。
- 将第一个向量 (v_1) 正规化，得到正交基的第一个向量 (u_1 = v_1)。
- 对于每个后续向量 (v_k)（其中 (k = 2, 3, ..., n)），减去它在之前所有正交向量 (u_1, u_2, ..., u_{k-1}) 上的投影，得到一个新的向量 (u_k)： [ u_k = v_k - \sum_{j=1}^{k-1} \frac{\langle v_k, u_j \rangle}{\langle u_j, u_j \rangle} u_j ]
- 将每个 (u_k) 正规化，得到标准正交基 ({e_1, e_2, ..., e_n})，其中 (e_k = \frac{u_k}{|u_k|})。
通过格拉姆-施密特正交化过程，你可以将任何一组线性无关的向量转换成一组正交或标准正交的向量集合。这一过程在许多数学和工程领域都有应用，包括线性代数、泛函分析、量子力学等。
图片来源：百度百科