参考资料

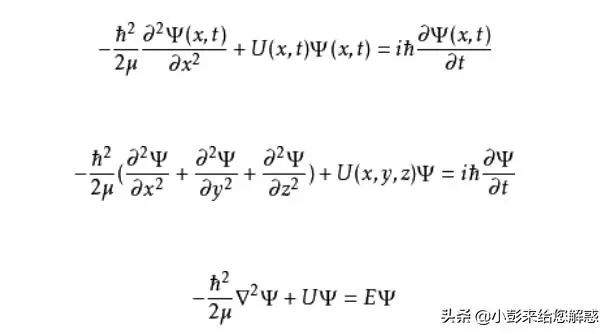
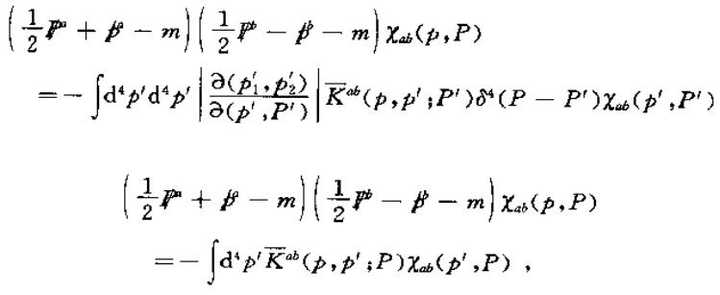
Moonshot回答
贝特-萨尔皮特方程(Bethe-Salpeter Equation,简称BSE)与非相对论性的束缚态方程主要有以下区别:
-
相对论性与非相对论性:贝特-萨尔皮特方程是一个相对论性方程,它在量子场论框架下描述束缚态,考虑了粒子的相对论性效应。而非相对论性束缚态方程,如薛定谔方程,不考虑相对论效应,适用于速度远低于光速的粒子。
-
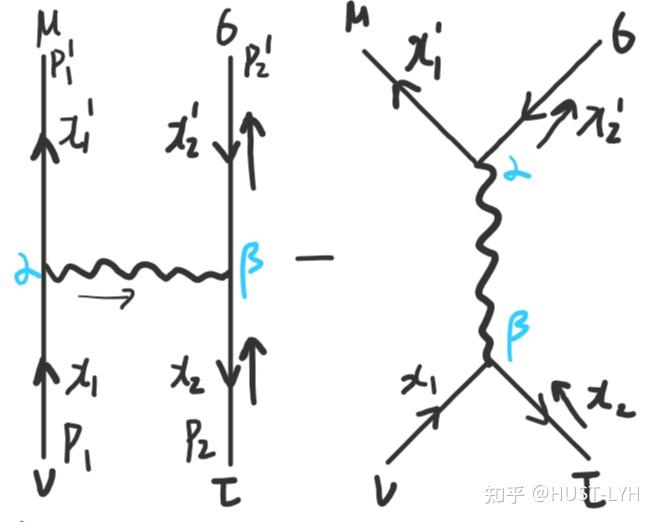
多粒子系统:贝特-萨尔皮特方程专门用于描述多粒子系统中的束缚态,如电子-空穴对在固体物理中。而非相对论性方程通常描述单个粒子在势场中的运动。
-
粒子的不可区分性:贝特-萨尔皮特方程考虑了粒子的不可区分性,这对于费米子系统(如电子)非常重要。非相对论性方程通常不考虑这一点。
-
数学结构:贝特-萨尔皮特方程是一个复杂的非齐次积分方程,其数学结构比非相对论性方程复杂得多。这种复杂性是为了超越微扰论,更准确地描述粒子间的相互作用。
-
应用领域:贝特-萨尔皮特方程广泛应用于粒子物理学、凝聚态物理学等领域,而非相对论性束缚态方程更多用于原子物理学和分子物理学。
总的来说,贝特-萨尔皮特方程提供了一个更为全面和精确的框架来描述相对论性多粒子系统的束缚态,尤其是在粒子间存在强相互作用时。而非相对论性束缚态方程则适用于更简单的情况,如单个粒子在势场中的运动。
继续提问
相关问题
贝特–萨尔皮特方程与其他描述相对论束缚态的方程(比如Dirac方程)相比有什么优缺点?
贝特–萨尔皮特方程在其他领域(例如凝聚态物理)中是否也有应用?具体体现在哪些方面?
贝特–萨尔皮特方程在量子场论中用于描述什么类型的物理现象?
如何进行贝特–萨尔皮特方程的数值求解?常用的数值方法有哪些?
布尔夏德三世与奥托一世的关系如何影响了他的政治生涯?
18世纪的新古典主义艺术风格如何影响了中国和印度的宫廷艺术?
权健集团在2019年因涉嫌传销活动被调查的事件是如何展开的?
《Vermeer's Hat》为何能获得马克·林顿历史奖?
弗拉基米尔一世·斯维亚托斯拉维奇是如何通过接受东正教将基辅罗斯引入欧洲基督教政治圈的?
715年,唐朝的皇帝是谁?