在不同维度下,Ising模型的可解析解与计算复杂性有何差异?
参考资料


参考资料



Moonshot回答
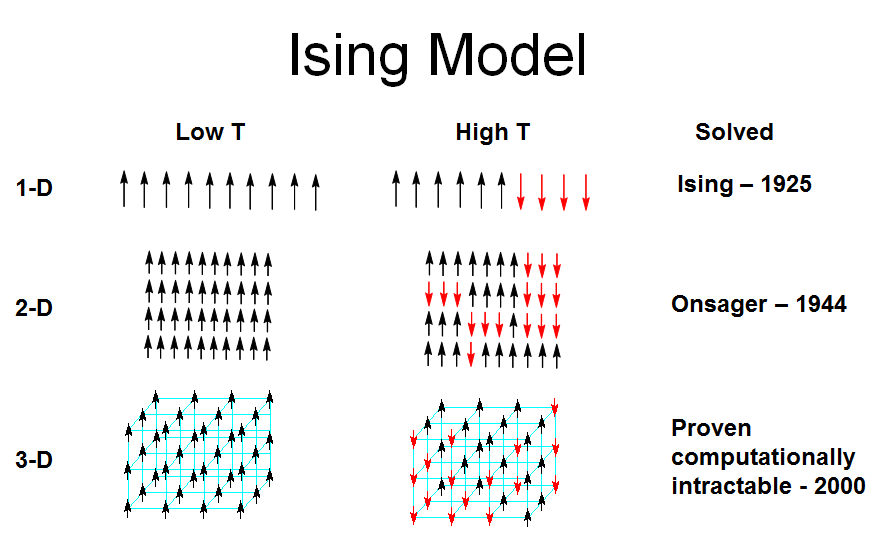
Ising模型是一个在统计物理中用来描述铁磁相变等现象的数学模型,它在不同维度下展现出不同的可解析性和计算复杂性。
在一维Ising模型中,由于其简单性,可以得到精确的解析解。一维Ising模型的配分函数可以被精确计算,从而得到模型的热力学性质,例如自由能、磁化率和比热容等。一维模型的解析解揭示了其相变行为,例如在临界温度以下,系统会发生相变,从无序相转变为有序相。
然而,在二维Ising模型中,尽管没有外部磁场时也可以得到精确的解析解,但这些解是通过复杂的数学方法得到的,例如利用共形场理论和二维统计物理中的精确可解性。二维Ising模型的解析解揭示了其临界现象和普适性,例如在临界点附近,系统的物理量会按照幂律变化,显示出无标度性。
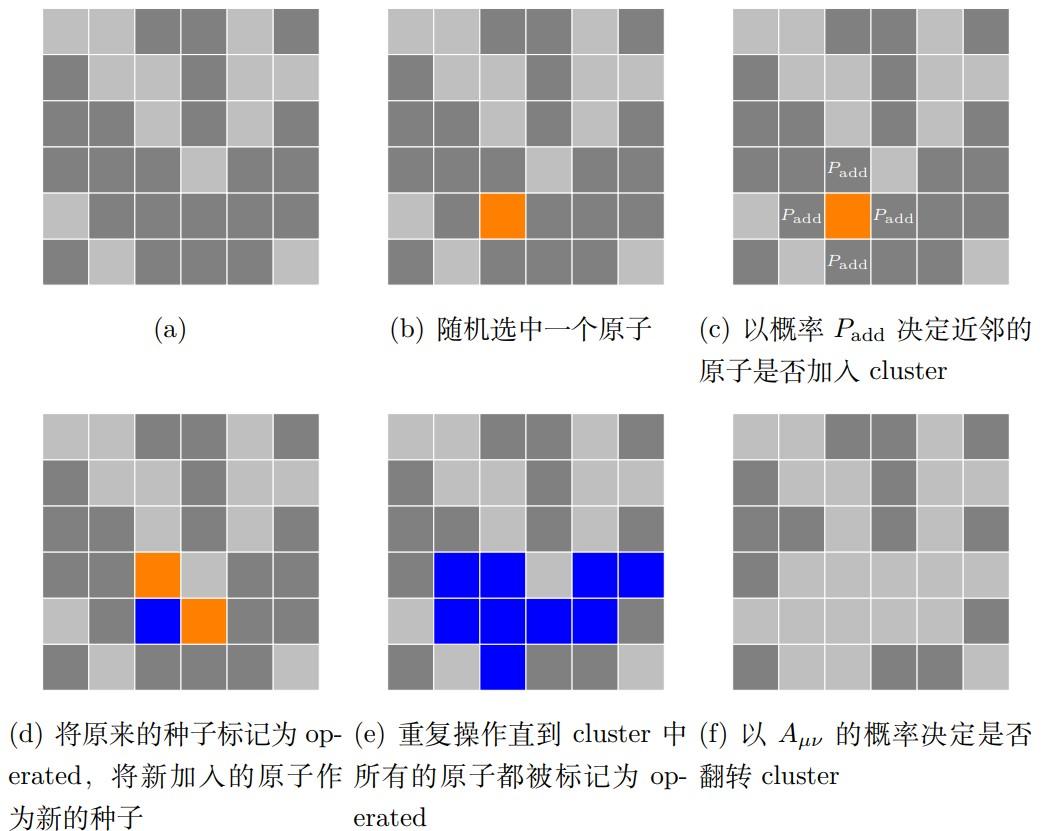
对于三维和更高维度的Ising模型,精确的解析解变得难以获得。这些模型的计算复杂性显著增加,通常需要借助数值模拟和近似方法来研究。例如,可以使用蒙特卡洛模拟来研究三维Ising模型的相变和临界现象。这些数值方法虽然不能提供精确的解析解,但可以给出非常精确的物理量的估计。
总的来说,Ising模型在不同维度下的可解析性和计算复杂性有显著差异。一维模型相对简单,可以得到精确的解析解;而高维模型,尤其是三维模型,通常需要数值模拟和近似方法来研究。这些模型的解析解和数值研究对于理解相变、临界现象以及复杂系统的行为都具有重要意义。