泊松分布的参数是什么,它在统计学中的应用场景有哪些?
参考资料
参考资料

Moonshot回答
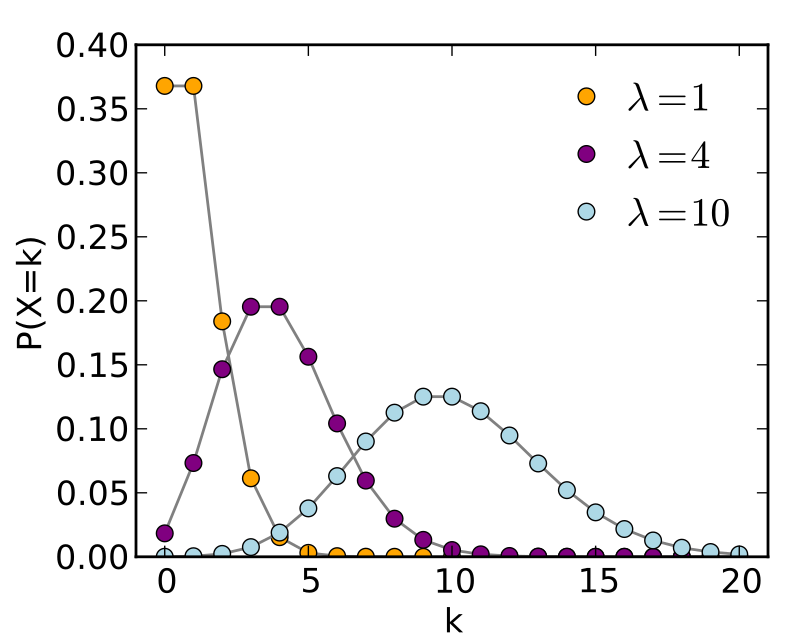
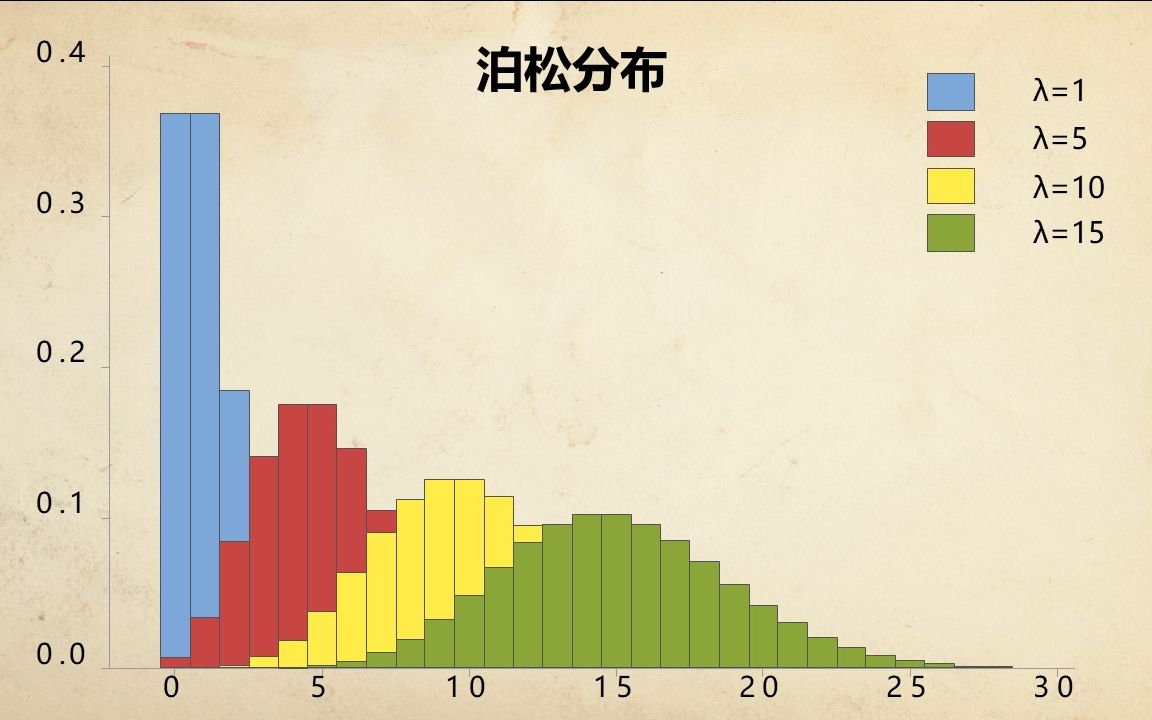
泊松分布的参数是单一参数λ(lambda),它代表事件在单位时间或单位空间内发生的平均次数,也称为速率参数。泊松分布的概率质量函数由下式给出:
[ P(X=k) = \frac{e^{-\lambda} \lambda^k}{k!} ]
其中,( k ) 是事件的发生次数,( e ) 是自然对数的底数。
泊松分布在统计学中的应用场景非常广泛,包括但不限于:
- 描述在特定时间间隔内通过特定点的车辆数量:例如,一个小时内通过某个路口的车辆数。
- 模拟服务台的顾客到达情况:如银行柜台前顾客的到达频率。
- 模拟在一定时间内发生保险索赔的次数:保险公司常用泊松分布来预测在一定时间内的索赔次数。
- 模拟顾客到达队列的情况:在排队理论中,泊松分布可以模拟顾客到达的频率,帮助设计更有效的服务系统。
- 印刷错误数和交通事故次数:在质量控制和风险评估中,泊松分布可以用来预测一定样本中缺陷或事故的发生次数。
泊松分布之所以在这些场景中得到广泛应用,是因为它能够很好地模拟那些在固定时间或空间内随机且独立发生的事件。通过泊松分布,我们可以对这些随机事件的发生概率进行估计和预测。