如何通过马克斯韦方程组推导出电场和磁场的波动方程?
参考资料


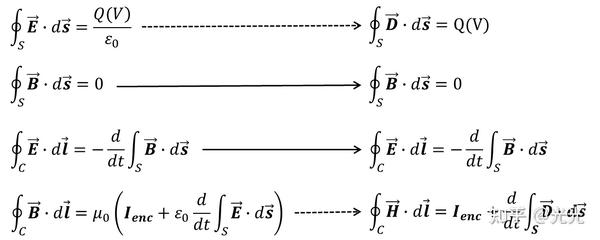
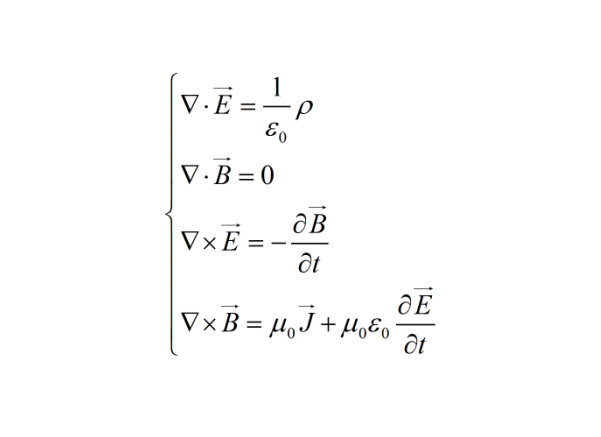
Moonshot回答
通过马克斯韦方程组推导出电场和磁场的波动方程的过程如下:
-
从麦克斯韦方程组的四个方程开始,其中涉及电场 ( \mathbf{E} ) 和磁场 ( \mathbf{B} ),以及电荷密度 ( \rho ) 和电流密度 ( \mathbf{J} )。
-
在没有电荷和电流的情况下(即 ( \rho = 0 ) 和 ( \mathbf{J} = 0 )),方程组简化为:
- ( \nabla \cdot \mathbf{E} = 0 )
- ( \nabla \cdot \mathbf{B} = 0 )
- ( \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} )
- ( \nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} )
-
对第三个方程取旋度,并将第四个方程代入,得到:
- ( \nabla \times (\nabla \times \mathbf{E}) = -\mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} )
-
使用向量恒等式 ( \nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A} ),由于 ( \nabla \cdot \mathbf{E} = 0 ),得到:
- ( -\nabla^2 \mathbf{E} = -\mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} )
- ( \nabla^2 \mathbf{E} = \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} )
-
同理,对第四个方程取旋度并代入第三个方程,可以得到电场的波动方程:
- ( \nabla^2 \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{B}}{\partial t^2} )
这样,我们就得到了电场和磁场的波动方程,表明在没有电荷和电流的情况下,电场和磁场以波的形式在空间中传播,传播速度为光速 ( c = \frac{1}{\sqrt{\mu_0 \epsilon_0}} )。这一理论由麦克斯韦在1864年提出,并由赫兹在1887年通过实验验证。