量子力学中的对易关系与经典物理学中的变量关系有什么不同？
参考资料
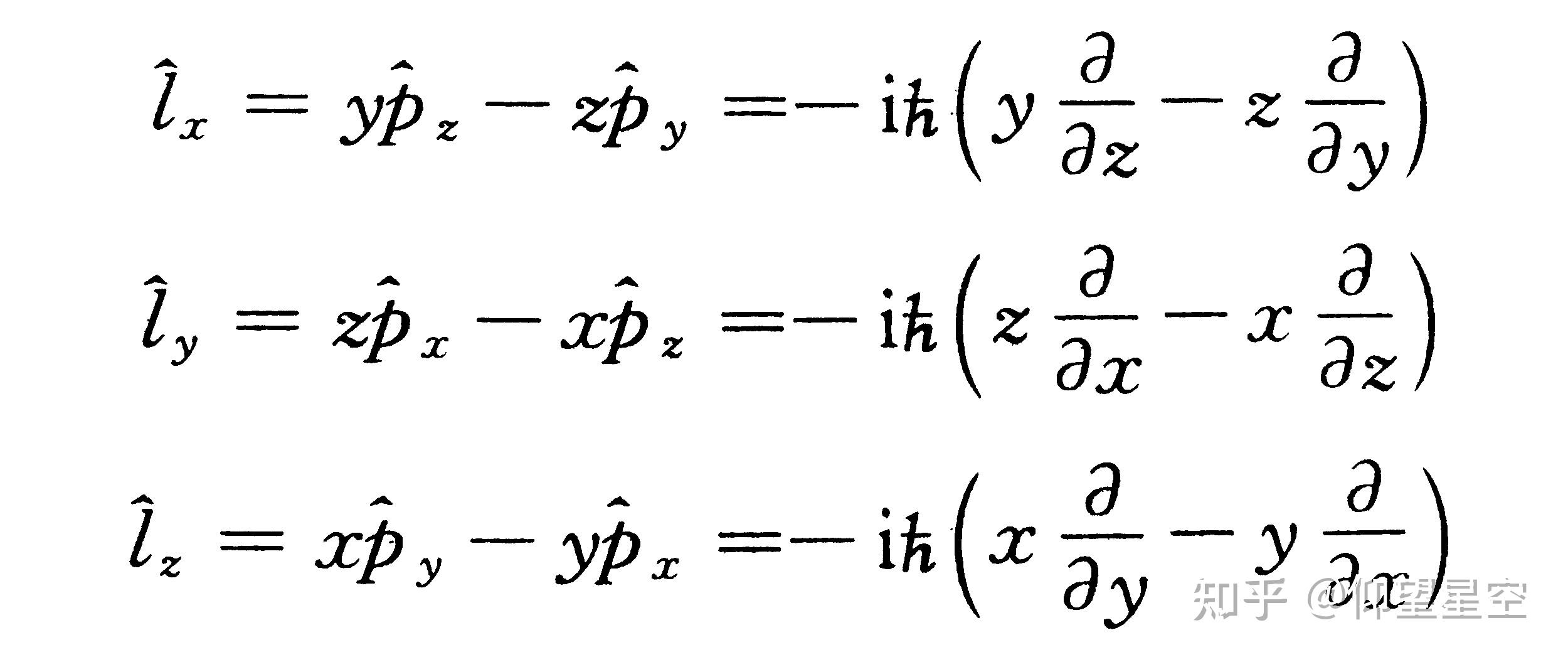
参考资料
Moonshot回答
在量子力学中，对易关系是描述算符（如位置和动量算符）相互作用的基本规则。两个算符A和B的对易子定义为 ([A, B] = AB - BA)。如果两个算符的对易子为零，即 ([A, B] = 0)，这意味着这两个算符可以交换顺序，这在经典物理学中是常见的。然而，在量子力学中，许多基本的物理量，如位置和动量，其对应的算符并不对易，例如，位置算子X和动量算子P满足对易关系 ([X, P] = i\hbar)，其中 (\hbar) 是约化普朗克常数。这表明在量子力学中，测量一个物理量可以影响另一个物理量的值，这是由海森堡不确定性原理所描述的，而在经典物理学中，这样的不确定性并不存在。
经典物理学中的变量关系通常遵循确定性原理，即如果初始条件已知，那么系统的后续状态可以被完全预测。这与量子力学中的概率性描述形成鲜明对比，在量子力学中，一个量子系统的态由波函数描述，而测量的结果则是概率性的，由波函数的绝对值的平方给出。
总的来说，量子力学中的对易关系揭示了量子世界中物理量的非对易性和不确定性，而经典物理学中的变量关系则是确定性的，并且遵循牛顿力学的规律。这种根本的区别是量子力学与经典物理学之间的一个核心差异。