巴拿赫空间和欧几里得空间有什么区别和联系?
参考资料



参考资料



参考资料


Moonshot回答
巴拿赫空间和欧几里得空间都是数学中的重要概念,但它们在定义、性质和应用方面存在一些区别和联系。
巴拿赫空间是泛函分析中的一个核心概念,它是一个完备的赋范向量空间。这意味着巴拿赫空间中的每一个柯西序列都收敛于该空间内的某一点。巴拿赫空间可以是有限的,也可以是无限的维数,并且可以定义在实数或复数域上。巴拿赫空间在函数空间、算子理论和微分方程等领域都有广泛的应用。
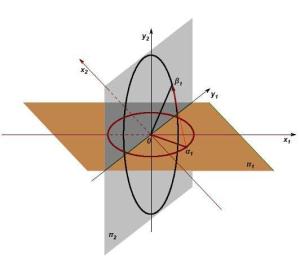
欧几里得空间则是几何学中的一个基本概念,它是一个有限维的实内积空间。我们通常所说的二维平面和三维空间都是欧几里得空间的例子。在欧几里得空间中,可以定义长度、角度和面积等几何概念,它是我们日常生活中最直观的空间模型。
区别:
- 维数:欧几里得空间是有限维的,而巴拿赫空间可以是无限维的。
- 完备性:巴拿赫空间强调的是完备性,即空间中的柯西序列都收敛于空间内某一点;而欧几里得空间的完备性是隐含的,因为它是有限维的。
- 应用领域:巴拿赫空间更多地应用于泛函分析和函数空间,而欧几里得空间则更多地应用于几何学和直观的空间建模。
联系:
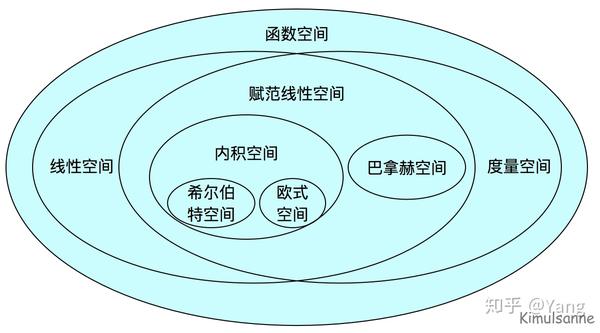
- 欧几里得空间可以看作是巴拿赫空间的一个特例,即当巴拿赫空间的维数有限且定义在实数域上时,它就是一个欧几里得空间。
- 两者都强调了空间中元素的“距离”概念,无论是通过范数还是通过内积,都可以在这些空间中定义元素之间的距离。
总的来说,巴拿赫空间和欧几里得空间在数学中都扮演着重要的角色,它们各自有着独特的性质和应用,但也存在着一定的联系。通过了解这些区别和联系,我们可以更好地理解数学中的各种空间概念,并在实际问题中加以应用。