拉格朗日密度中的复合电磁四矢势由哪些广义电磁势构成,这些势分别代表什么?
参考资料
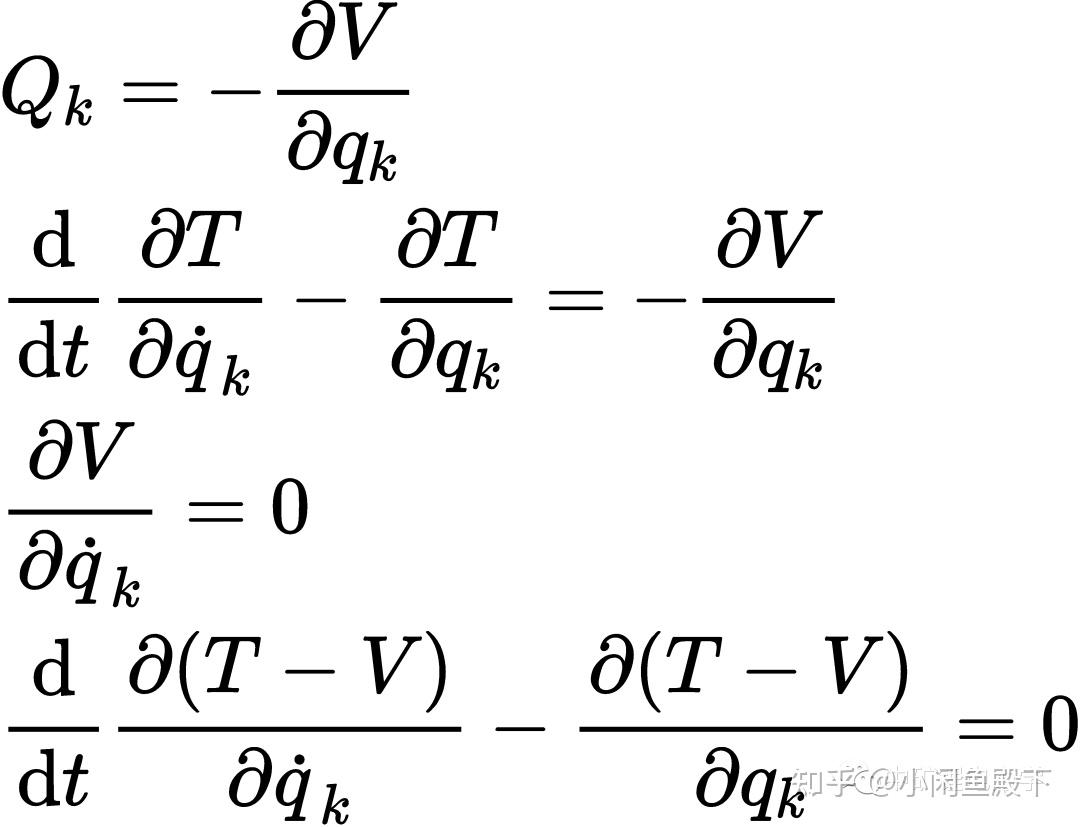
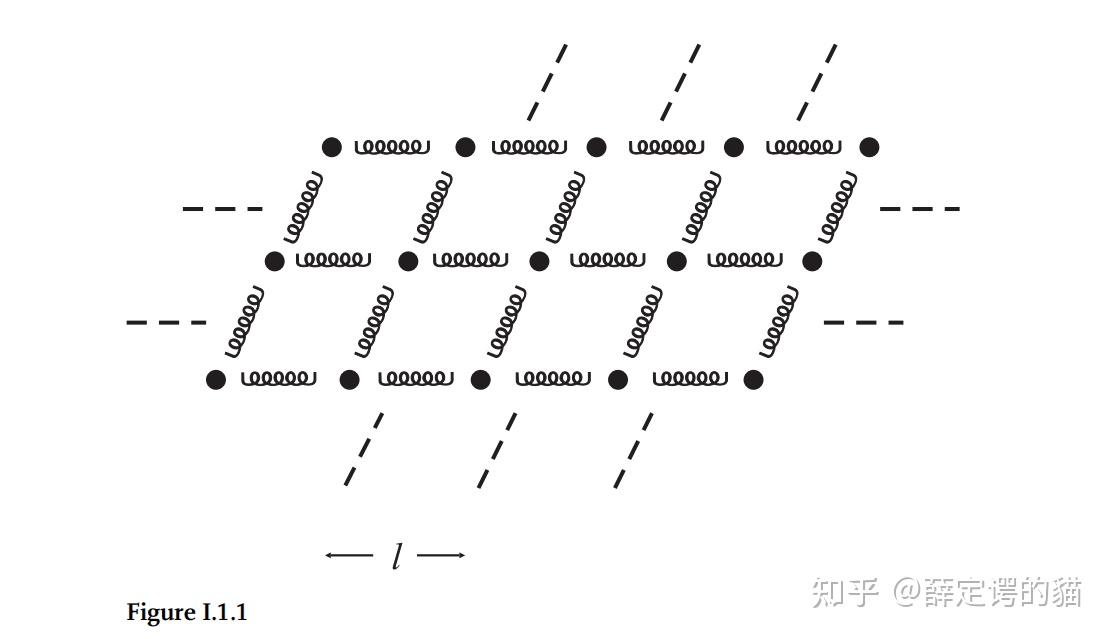

参考资料
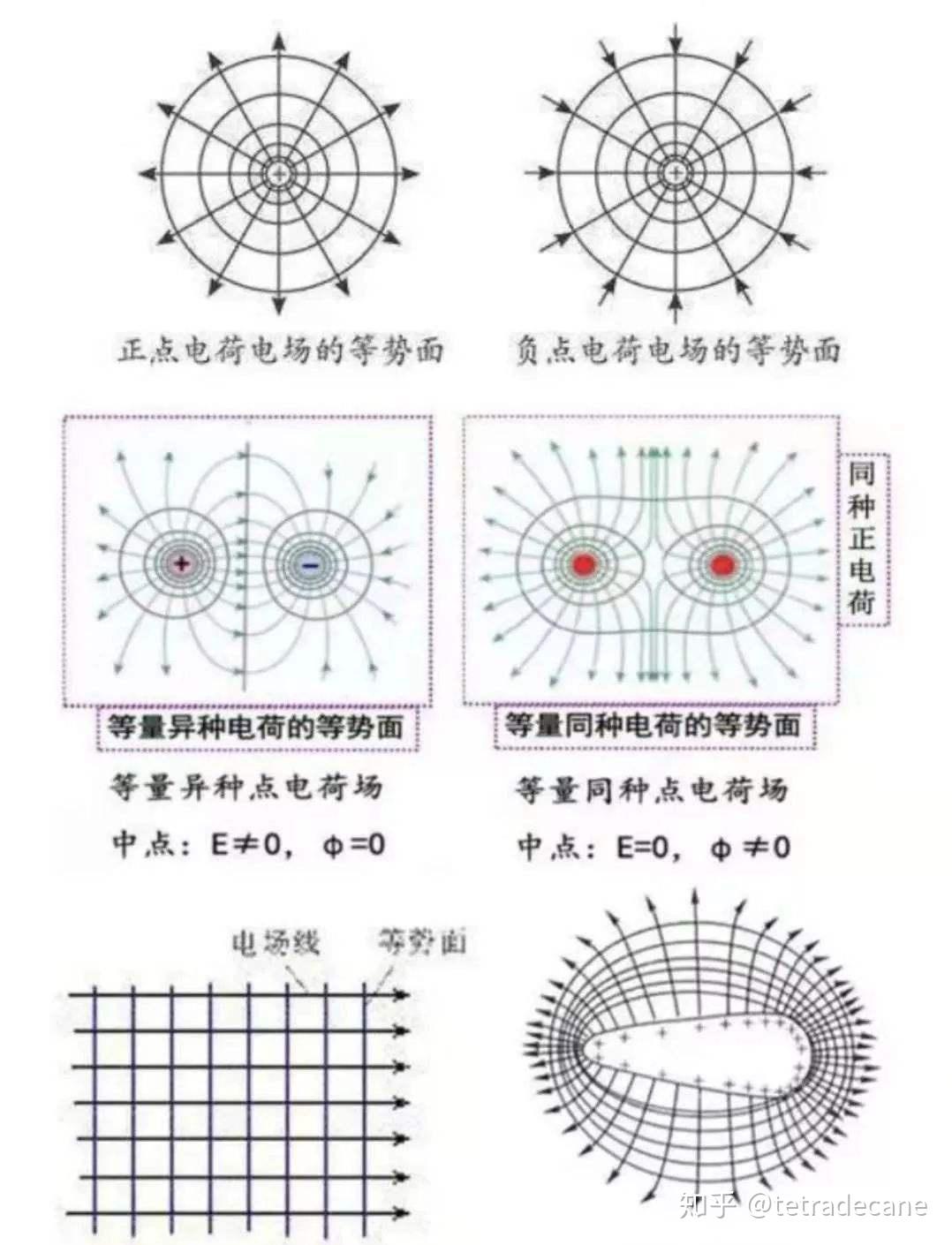
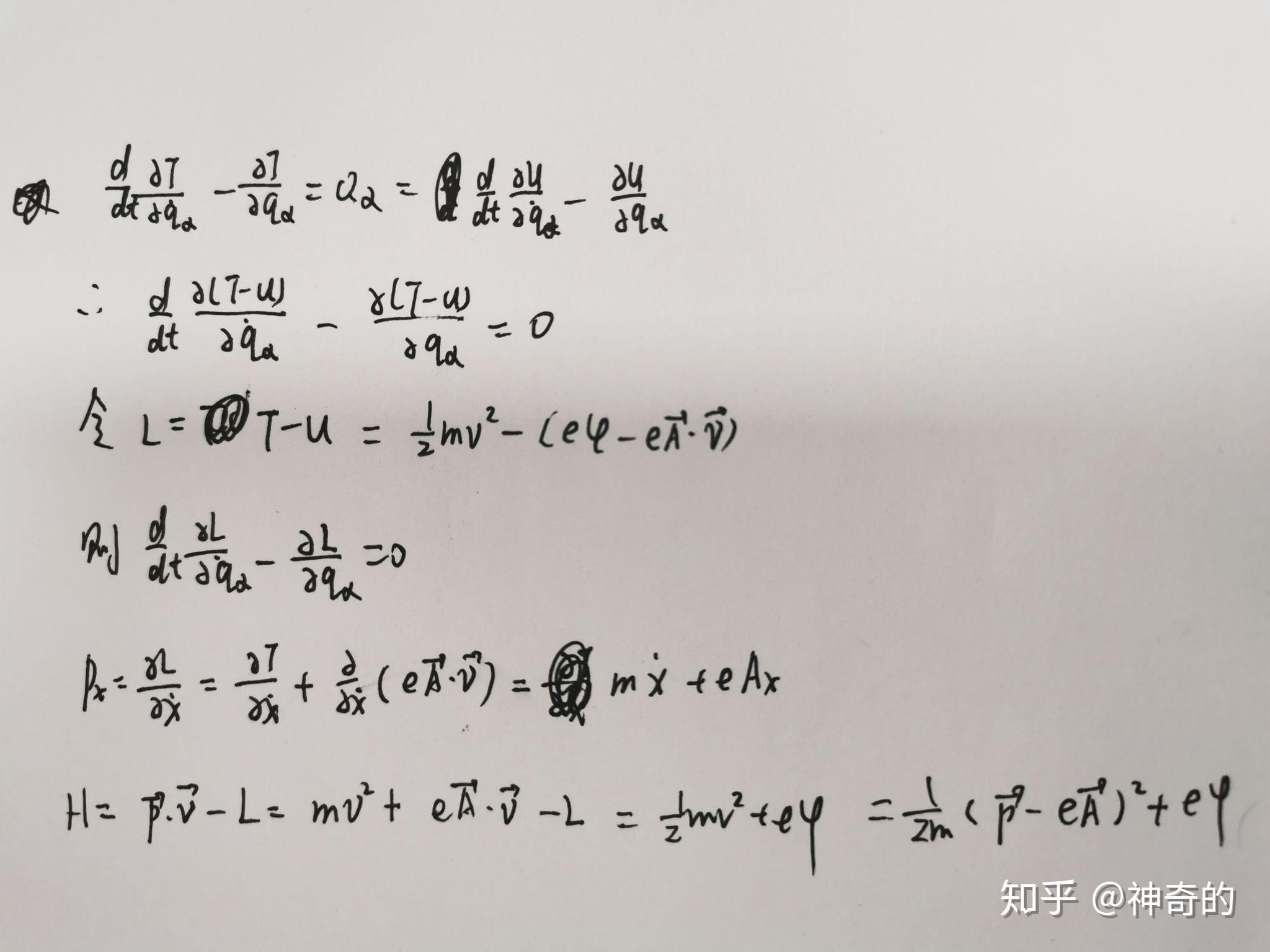
Moonshot回答
拉格朗日密度中的复合电磁四矢势由广义电势 ( A_0 )(标势或电势)和广义磁矢势 ( \mathbf{A} )(磁矢势)构成。在电磁学中,复合电磁四矢势 ( A_\mu ) 表示为 ( A_\mu = (A_0, \mathbf{A}) ),其中 ( A_0 ) 对应于电势,而 ( \mathbf{A} ) 对应于磁矢势。
广义电势 ( A_0 ) 代表电势,它与电场 ( \mathbf{E} ) 的关系为 ( \mathbf{E} = -\nabla A_0 - \frac{\partial \mathbf{A}}{\partial t} )。广义磁矢势 ( \mathbf{A} ) 代表磁矢势,它与磁场 ( \mathbf{B} ) 的关系为 ( \mathbf{B} = \nabla \times \mathbf{A} )。
在拉格朗日密度中,电磁场的拉格朗日密度可以写为 ( \mathcal{L} = -\frac{1}{4}F_{\mu\nu}F^{\mu\nu} + \mathcal{L}m ),其中 ( F{\mu\nu} ) 是电磁场张量,由 ( F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu ) 给出。这个拉格朗日密度描述了电磁场的动力学,并且可以用来导出麦克斯韦方程。
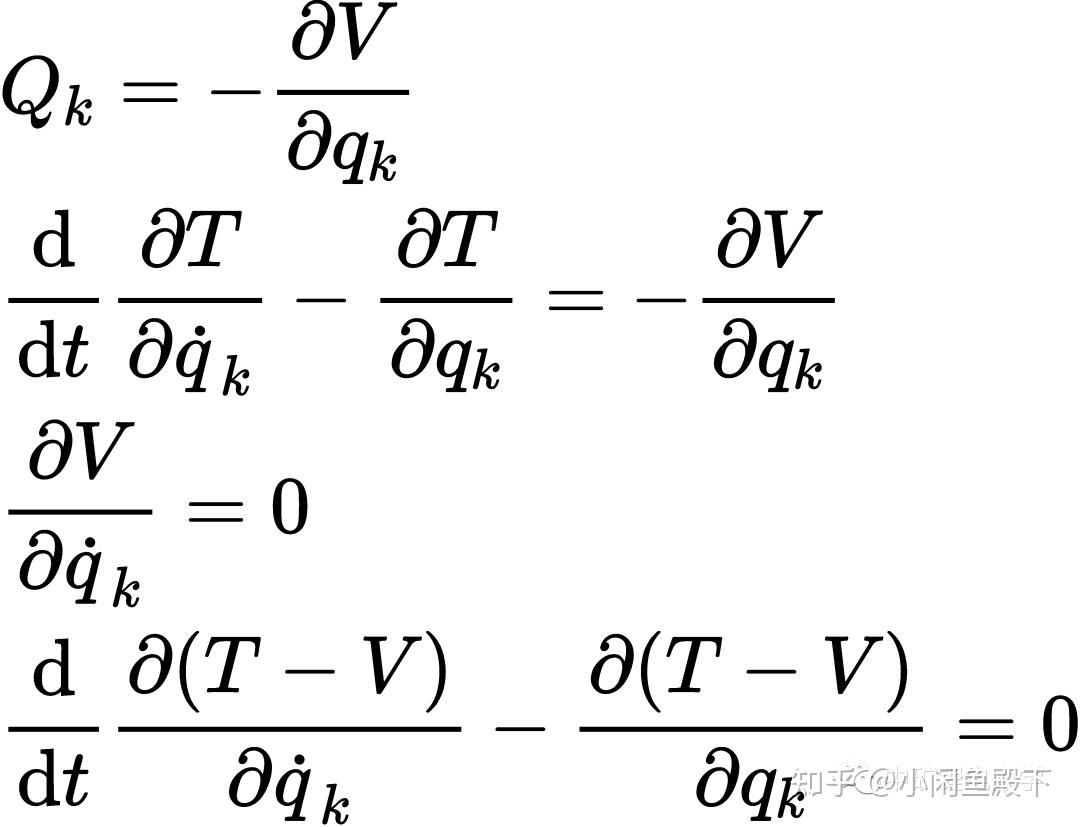
这张图展示了电磁四矢势的概念。通过搜索结果,我们可以看到拉格朗日密度中复合电磁四矢势的构成和各个势代表的物理量。广义电势和磁矢势在电磁场的拉格朗日表述中扮演着基础的角色,它们是构建电磁场动力学的关键要素。