参考资料

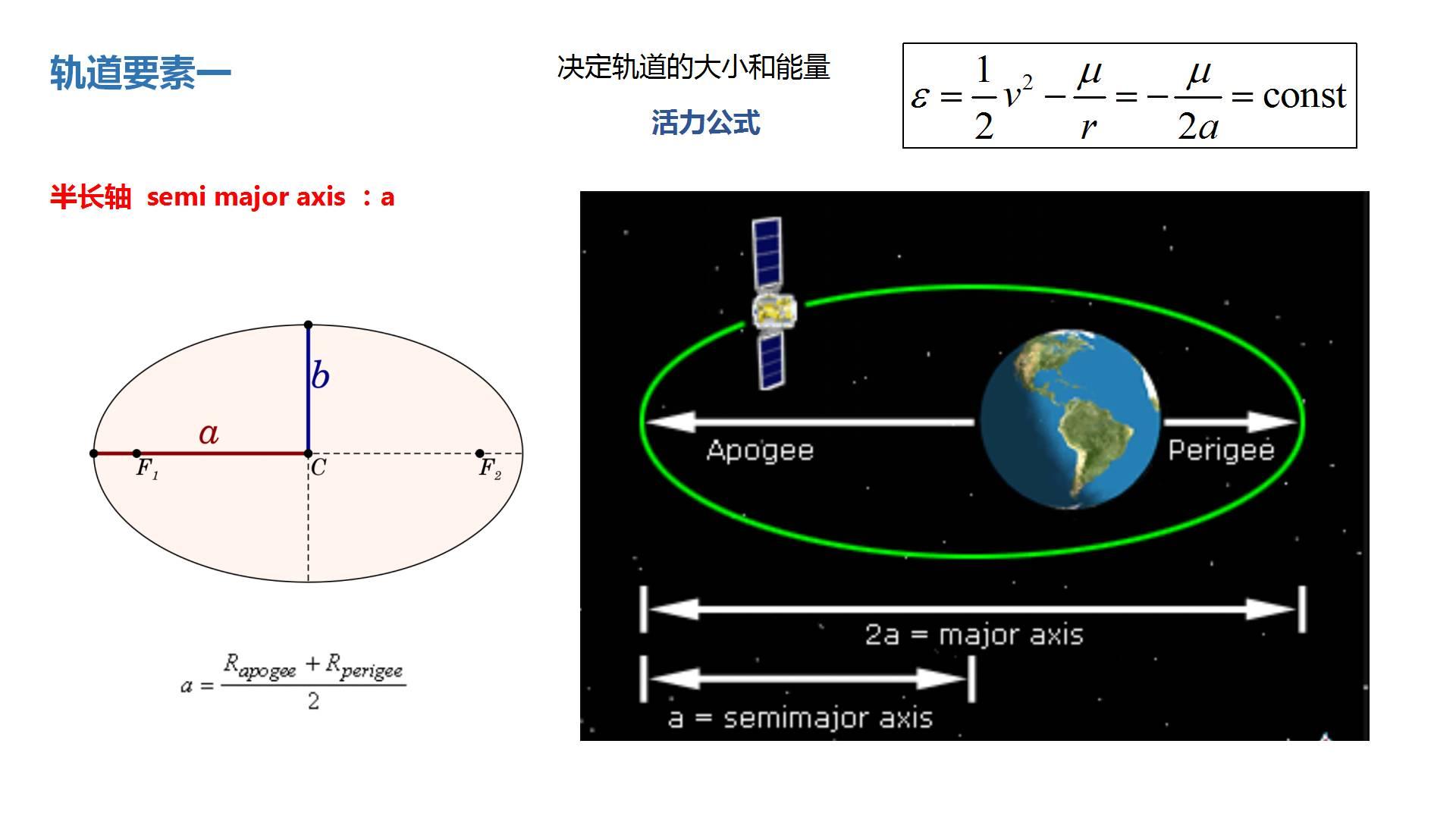
轨道周期是指一个天体绕中心天体（如行星绕太阳）完成一次公转所需的时间。轨道周期与轨道的半长轴和离心率有直接关系，可以通过开普勒第三定律来描述。根据这个定律，一个行星的轨道周期的平方与其轨道半长轴的立方成正比。公式可以表示为：

[ T^2 = \frac{4\pi^2}{G(M+m)}a^3 ]

其中：

• ( T ) 是轨道周期，
• ( G ) 是万有引力常数，
• ( M ) 是中心天体的质量，
• ( m ) 是绕行天体的质量，
• ( a ) 是轨道的半长轴。

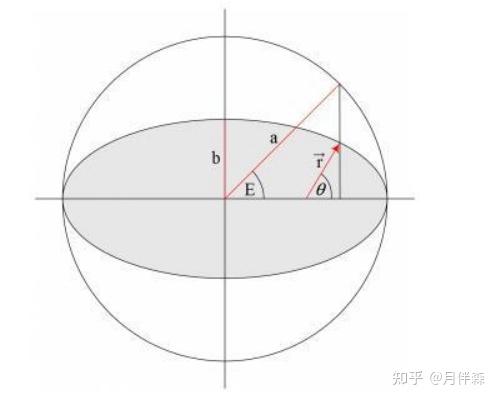
轨道的离心率 ( e ) 描述了轨道的形状，其值介于0（圆形）和1（抛物线或双曲线）之间。对于椭圆轨道，离心率越小，轨道越接近圆形；离心率越大，轨道越扁平。轨道的半长轴 ( a )、离心率 ( e ) 和轨道周期 ( T ) 之间的关系可以通过开普勒第三定律来联系。

图片来源：网络

从搜索结果中，我们可以看到半长轴相同的椭圆轨道具有相同的轨道周期，而轨道的离心率则影响轨道的形状，但不影响轨道周期。所有行星的轨道半长轴的三次方与其公转周期的二次方的比值相等，这体现了开普勒第三定律。因此，轨道周期主要取决于轨道的半长轴，而与离心率无关。