什么是广义动量,它在哈密顿量中如何体现?
参考资料

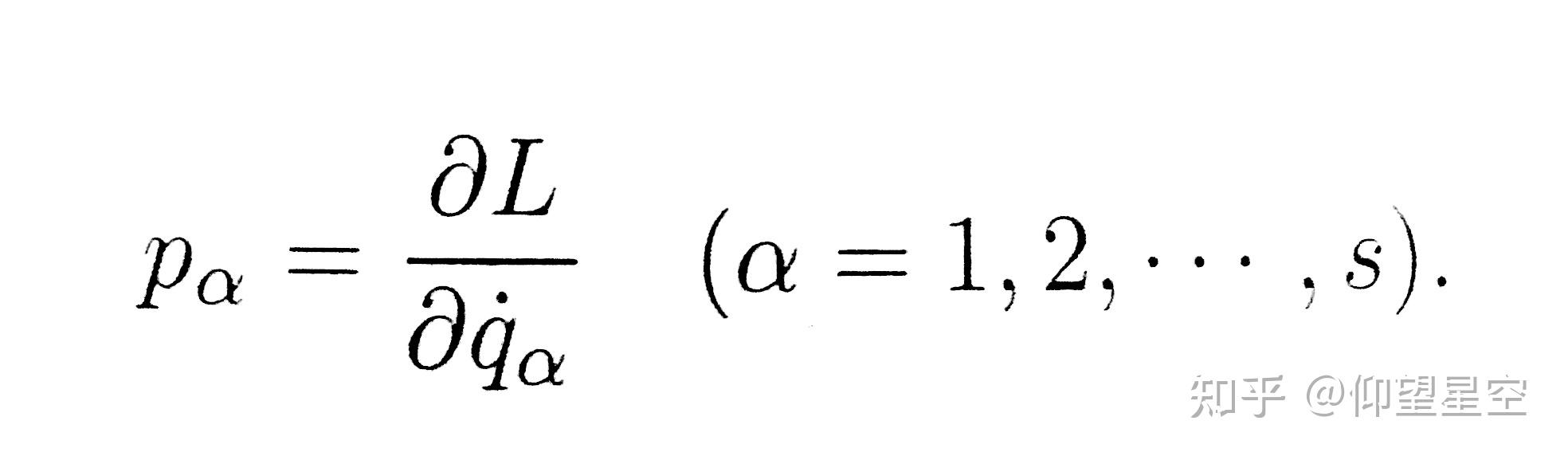


Moonshot回答
广义动量是分析力学中的一个重要概念,它在哈密顿力学中扮演着核心角色。广义动量定义为拉格朗日量对广义速度的偏导数,即 ( p_j = \frac{\partial L}{\partial \dot{q}_j} ),其中 ( L ) 是拉格朗日量,( \dot{q}_j ) 是广义速度。在哈密顿力学中,广义动量是正则共轭于广义坐标的物理量,也称为共轭动量。
哈密顿力学的目标是用广义动量变量取代广义速度,从而简化特定系统的表述,例如量子力学的某些方面。对于每个广义速度,都有一个对应的共轭动量。哈密顿量 ( H ) 定义为拉格朗日量 ( L ) 的勒让德变换,即 ( H = \sum_i p_i \dot{q}_i - L ),其中 ( p_i ) 是广义动量,( \dot{q}_i ) 是广义速度。
广义动量和广义坐标是独立的,这使得哈密顿力学在处理约束系统时更为方便。哈密顿方程描述了系统状态随时间的演化,其中第一方程 ( \dot{q}_i = \frac{\partial H}{\partial p_i} ) 和第二方程 ( \dot{p}_i = -\frac{\partial H}{\partial q_i} ) 描述了广义坐标和广义动量的时间演化。

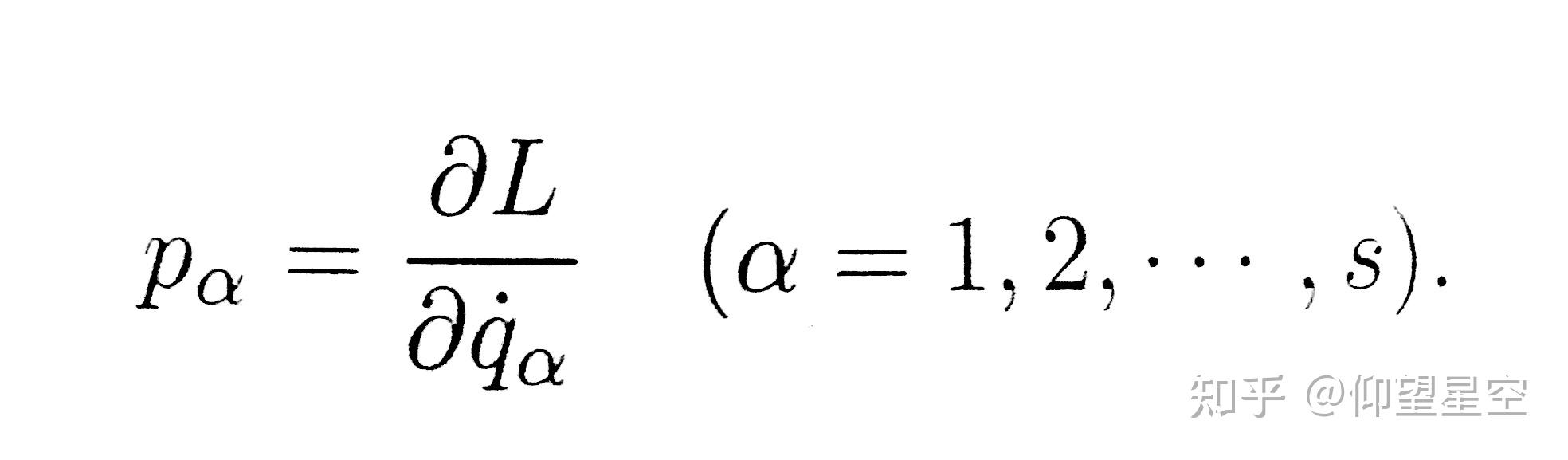
这些概念在物理学中非常重要,特别是在理论物理和量子力学中。广义动量和哈密顿量提供了一种描述物理系统动力学的有力工具。更多详细信息可以参考知乎上的相关专栏文章《从零开始的分析力学基础 4.广义动量》和维基百科上的《广义动量》和《哈密顿力学》。