高斯波包在量子力学中有什么重要性?
参考资料
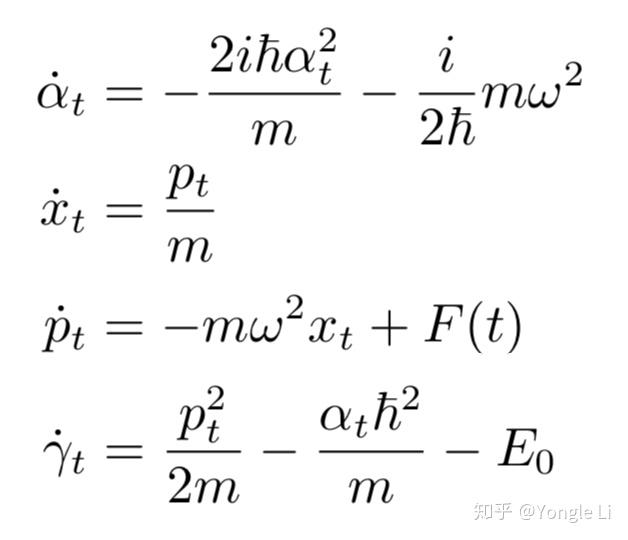
Moonshot回答
高斯波包在量子力学中具有重要性,主要体现在以下几个方面:
-
波粒二象性:高斯波包是粒子波函数的一种形式,能够表现出粒子和波动的双重性质,是波粒二象性的一个有力证据。[1]
-
简化模型:高斯波包是一个简单且对称性良好的模型,常用于描述粒子的初始状态,便于研究粒子在量子力学框架下的行为。[3]
-
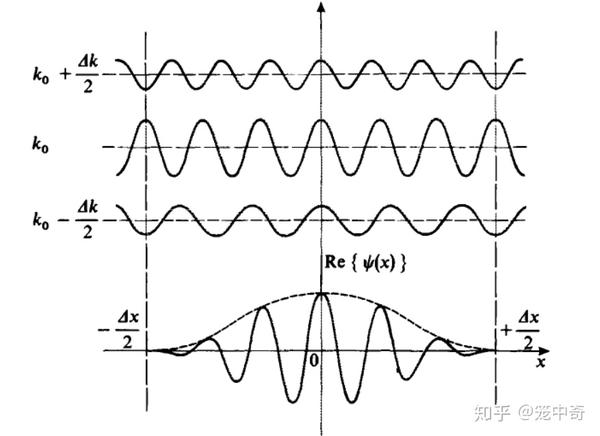
不确定性原理:高斯波包在位置和动量空间中具有特定的分布,其不确定性乘积接近于量子力学的极限,即满足海森堡不确定性原理。[4]
-
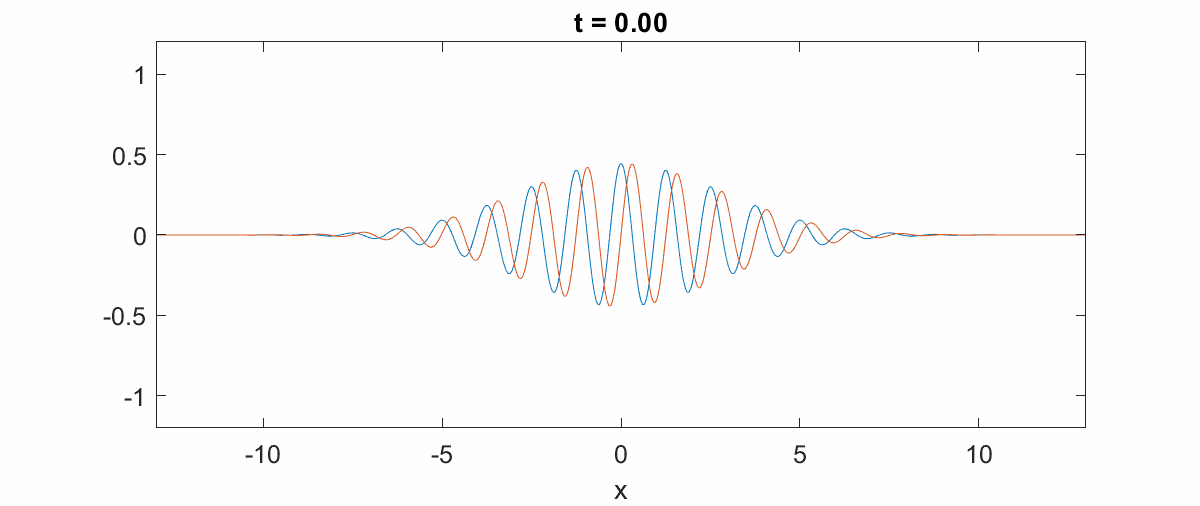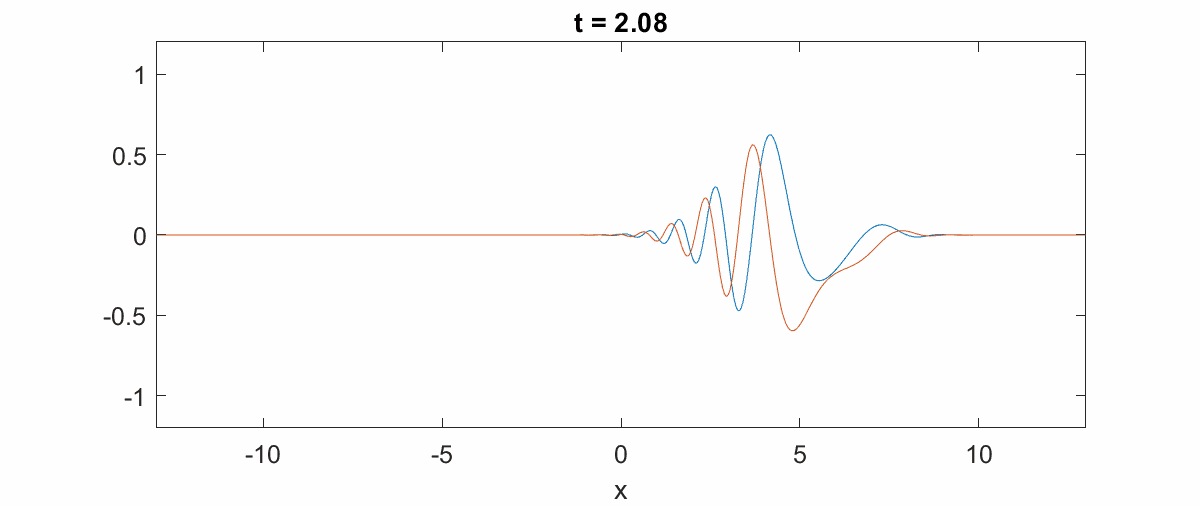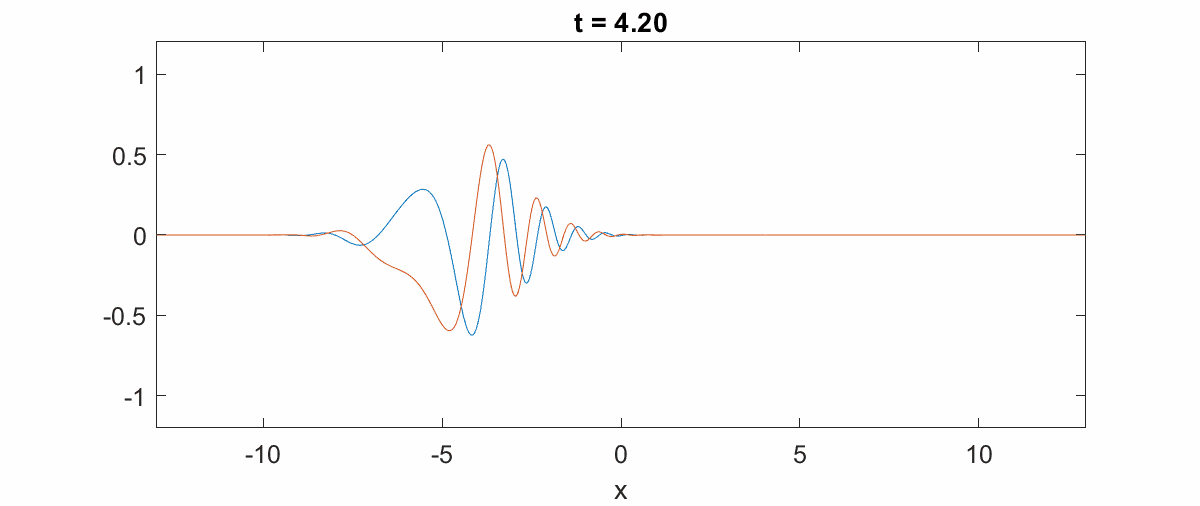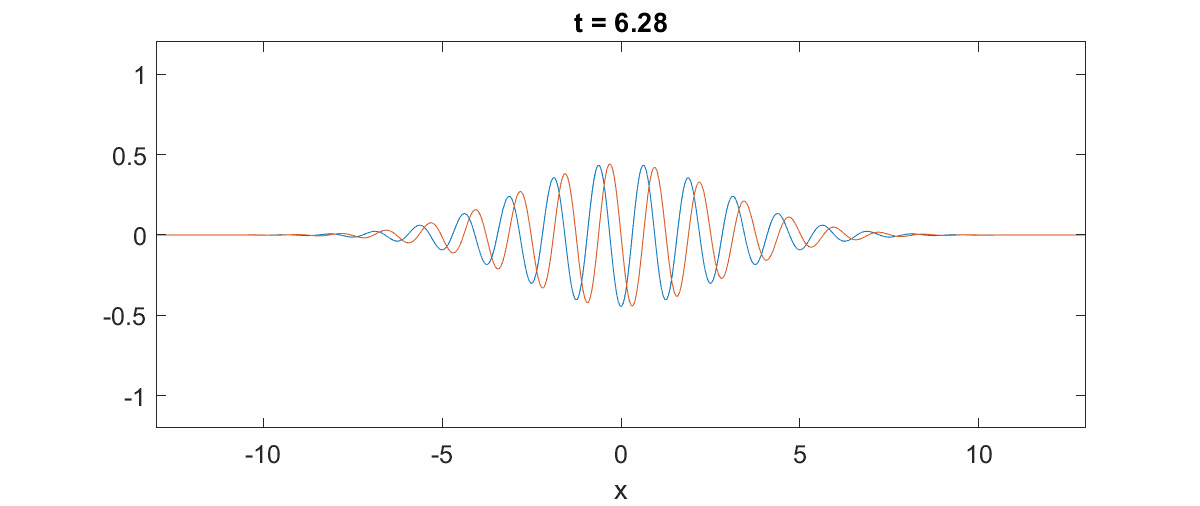
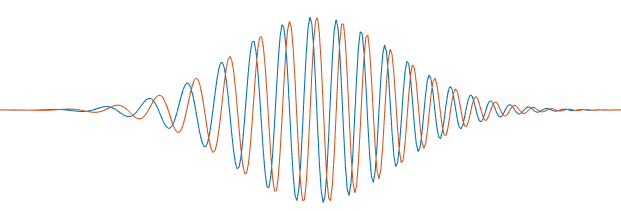
量子态的演化:高斯波包可以用来研究量子态随时间的演化,例如在自由空间中的扩散和在势场中的运动。[2]
-
实验验证:高斯波包因其特性,常被用于实验中以验证量子力学的预测,如量子干涉和量子纠缠现象。
-
应用广泛:在光学中,高斯波包可以描述激光脉冲的电场函数;在量子力学中,它被用作波函数,是研究量子系统的基础。
通过引用的搜索结果,我们可以看到高斯波包在量子力学中扮演着核心角色,不仅在理论研究中,在实验验证和实际应用中也非常重要。相关图像资料展示了高斯波包在不同情境下的表现,如量子谐振子的高斯波包演化和高斯波包的空间分布等。这些图像资料进一步直观地说明了高斯波包在量子力学中的重要性。