参考资料

在量子力学中，角动量守恒原理的体现与经典力学类似，但具有一些独特的量子特性。根据搜索结果，以下是一些关键点：

1. 对称性与守恒量的关系：量子力学中的对称性与守恒量之间存在直接联系。如果一个物理系统在某种对称操作下保持不变，那么相应的物理量就是守恒的。例如，如果一个系统在空间旋转下保持不变，那么角动量就是守恒的。这种对称性与守恒量的关系是量子力学的一个基本特征。

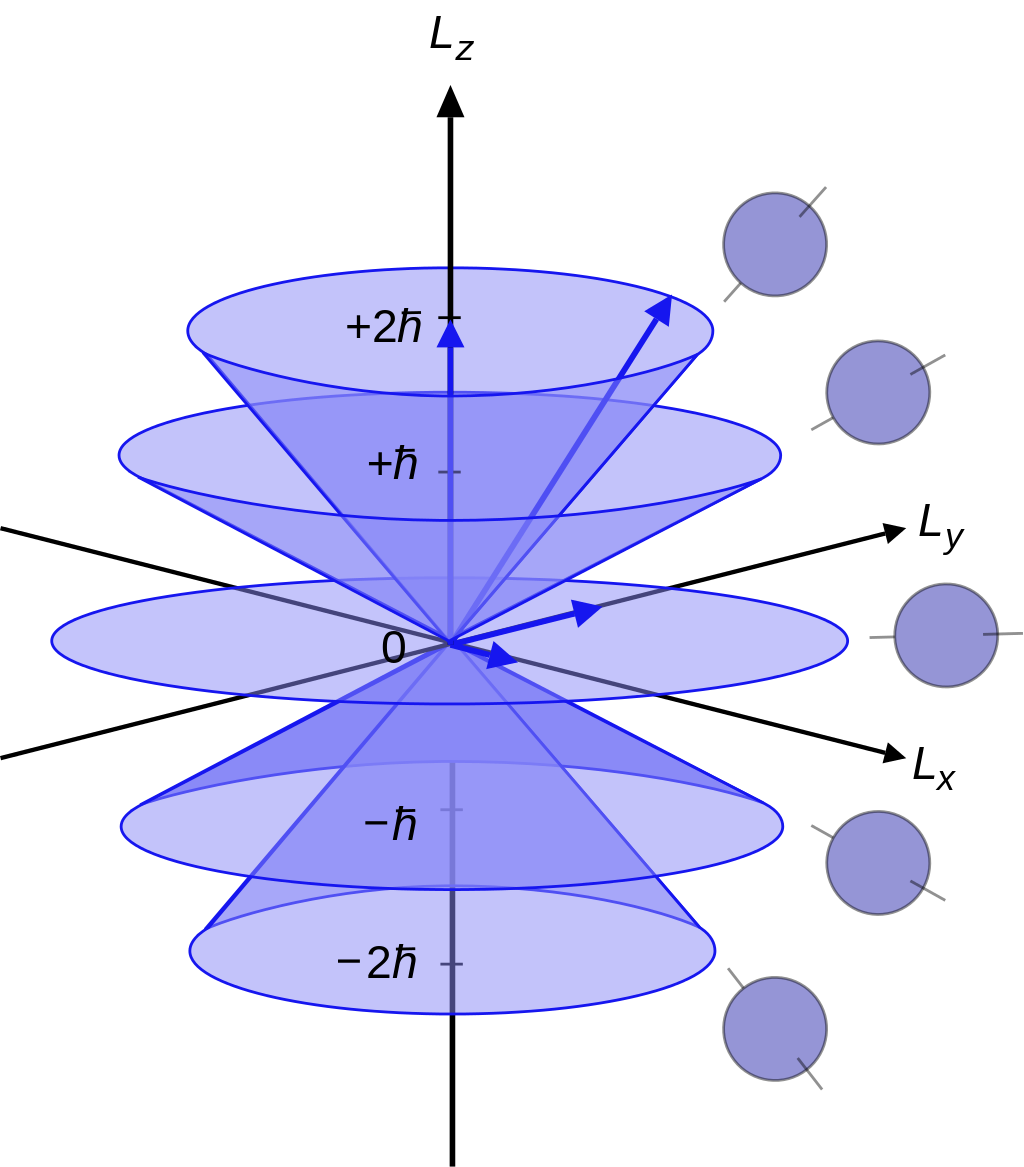
2. 角动量的量子化：在量子力学中，角动量是量子化的，这意味着它只能取特定的离散值。例如，一个粒子的总角动量可以表示为 (\mathbf{J} = \mathbf{L} + \mathbf{S})，其中 (\mathbf{L}) 是轨道角动量，(\mathbf{S}) 是自旋角动量。这些角动量的分量（如 (J_x), (J_y), (J_z)）只能取特定的量子化的值。

3. 角动量的守恒：在量子力学中，如果一个系统是孤立的，即没有外力矩作用，那么该系统的总角动量是守恒的。这与经典力学中的角动量守恒原理是一致的。例如，一个粒子在有心势场中的运动，其相对于势场中心的角动量是守恒的，这导致粒子的运动被限制在一个固定的平面内。

4. 角动量的代数结构：角动量的代数结构决定了角动量的本征值和本征态。在量子力学中，角动量的分量（如 (L_x), (L_y), (L_z)）满足特定的对易关系，这些关系决定了角动量的量子化特性和守恒性质。

5. 自旋角动量：在量子力学中，粒子的自旋角动量也是一个重要的概念。自旋是粒子的内禀角动量，与粒子的轨道运动无关。自旋角动量的引入进一步丰富了量子力学中角动量守恒的原理。

总的来说，角动量守恒原理在量子力学中得到了体现和扩展，不仅包括了经典力学中的角动量守恒，还引入了量子化和自旋等新的概念。这些特性使得量子力学中的角动量守恒原理更加丰富和精确。